题目内容
10.如图所示,在光滑水平桌面上的虚线MN左侧有方向竖直向上的匀强磁场,一质量为m、电阻为R、边长为L的正方形导体框静止在水平桌面上,且一条边框与MN平行.现对线框施加水平向右的恒力,线框从静止开始运动直到离开磁场,速度传感器记录了线框在该过程中速度随时间变化的v-t图线,图中v0,t0为已知量.求:(1)线框穿出磁场过程中电流强度I和通过线框的电量q;
(2)匀强磁场的磁感应强度B;
(3)若导体框初始位置不变,施加的恒力为原来的2倍,传感器测量到线框离开磁场前已经做匀速运动,则此情景下线框穿出磁场过程中产生电热Q.
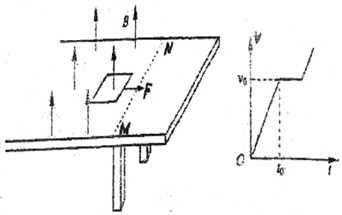
分析 (1)根据v-t图象求得力F作用时的加速度,由牛顿第二定律求得F的大小,再根据匀速出磁场的过程中拉力的功率与导体框的热功率相等求得穿出磁场过程中的电流大小,再根据Q=It求得电荷量;
(2)因为导体框匀速出磁场,故根据拉力与安培力相等求得磁感应强度的大小即可;
(3)当以拉力F作用时,在加速x0至速度为v0导体框开始出磁场,当以2F加速x0时速度达到v1导体框开始出磁场,当通过L的过程中,拉力F做的功一部分用来增大导体框的动能,一部分克服安培力做功(即为放出的热量),再根据匀速出磁场求得以2F出磁场时的速度,由能量守恒定律求解.
解答 解:(1)由v-t图象知,导体框在力F作用下产生的加速度a=$\frac{{v}_{0}}{{t}_{0}}$
因为导体框匀速离开磁场区域,故有:
F=ma=$m\frac{{v}_{0}}{{t}_{0}}$
因为匀速穿出磁场,故拉力F的功率等于导体框的热功率,故有:
$F{v}_{0}={I}^{2}R$
可得导体框穿出磁场时的电流
I=$\sqrt{\frac{F{v}_{0}}{R}}$=$\sqrt{\frac{m{v}_{0}^{2}}{R{t}_{0}}}$
导体框穿出磁场过程中通过导体框的电荷量
Q=It=$\sqrt{\frac{m{v}_{0}^{2}}{R{t}_{0}}}•\frac{L}{{v}_{0}}$=$\sqrt{\frac{m{L}^{2}}{R{t}_{0}}}$
(2)因为导体框匀速出磁场,故可得拉力F与安培力平衡即
F=m$\frac{{v}_{0}}{{t}_{0}}$=BIL
可得磁感应强度B=$\frac{m\frac{{v}_{0}}{{t}_{0}}}{\sqrt{\frac{m{v}_{0}^{2}}{R{t}_{0}}}L}$=$\frac{1}{L}\sqrt{\frac{mR}{{t}_{0}}}$
(3)拉力为F时,加速距离为x0,由题意满足:
$F{x}_{0}=\frac{1}{2}m{v}_{0}^{2}$
匀速离开磁场过程中有:
F-$\frac{{B}^{2}{L}^{2}{v}_{0}}{R}=0$
当拉力为2F时,在加速通过距离x0的过程中有:
$2F{x}_{0}=\frac{1}{2}m{v}_{1}^{2}$
离开磁场前达到匀速运动有:
2F-$\frac{{B}^{2}{L}^{2}{v}_{2}}{R}$=0
所以可得v2=2v0
所以根据能量守恒定律可知,在以2F拉力穿过磁场过程中有:
$2FL=Q+\frac{1}{2}m{v}_{2}^{2}-\frac{1}{2}m{v}_{1}^{2}$
联列解得:Q=$\frac{2m{v}_{0}L}{{t}_{0}}-m{v}_{0}^{2}$
答:(1)线框穿出磁场过程中电流强度I为$\sqrt{\frac{m{v}_{0}^{2}}{R{t}_{0}}}$和通过线框的电量q为$\sqrt{\frac{m{L}^{2}}{R{t}_{0}}}$;
(2)匀强磁场的磁感应强度B为$\frac{1}{L}\sqrt{\frac{mR}{{t}_{0}}}$;
(3)若导体框初始位置不变,施加的恒力为原来的2倍,传感器测量到线框离开磁场前已经做匀速运动,则此情景下线框穿出磁场过程中产生电热Q为$\frac{2m{v}_{0}L}{{t}_{0}}-m{v}_{0}^{2}$.
点评 本题是导体在导轨上滑动类型,要从力和能量两个角度分析答题,关键要掌握法拉第定律、欧姆定律、能量守恒等等基本规律,并能正确运用.

 阅读快车系列答案
阅读快车系列答案| A. | $\sqrt{7}$m/s | B. | 1 m/s | C. | $\sqrt{5}$m/s | D. | 5m/s |
 我国自行研制的新一代ZBL-09 8×8轮式步兵装甲车已达到国际领先水平,已成为中国军方快速部署型轻装甲部队的主力装备.该装甲车在平直的公路上从静止开始加速,经过较短的时间t和距离s速度便可达到最大值vm.设在加速过程中发动机的功率恒定为P,装甲车所受阻力恒为f,以下说法不正确的是( )
我国自行研制的新一代ZBL-09 8×8轮式步兵装甲车已达到国际领先水平,已成为中国军方快速部署型轻装甲部队的主力装备.该装甲车在平直的公路上从静止开始加速,经过较短的时间t和距离s速度便可达到最大值vm.设在加速过程中发动机的功率恒定为P,装甲车所受阻力恒为f,以下说法不正确的是( )| A. | 装甲车加速过程中,牵引力对它做功为Pt | |
| B. | 装甲车的最大速度vm=$\frac{P}{f}$ | |
| C. | 装甲车加速过程中,装甲车做加速度变小的加速直线运动 | |
| D. | 装甲车的质量 m=$\frac{2Pt}{{{v}_{m}}^{2}}$ |

| A. | 到达底端时两球的动能相等 | B. | 到达底端时两球重力的功率相等 | ||
| C. | 下滑过程两球重力所做的功不等 | D. | 下滑不同高度时两球的机械能相等 |
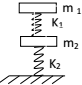 如图所示,两木块的质量分别为m1和m2,两轻质弹簧的劲度系数分别为k1和k2,上面木块压在上面的弹簧上(但不拴接),整个系统处于平衡状态.现缓慢向上提上面的木块,直到它刚离开上面弹簧.在这过程中上面木块移动的距离为( )
如图所示,两木块的质量分别为m1和m2,两轻质弹簧的劲度系数分别为k1和k2,上面木块压在上面的弹簧上(但不拴接),整个系统处于平衡状态.现缓慢向上提上面的木块,直到它刚离开上面弹簧.在这过程中上面木块移动的距离为( )| A. | $\frac{{m}_{1}g}{{k}_{1}}$ | B. | $\frac{{m}_{1}g}{{k}_{1}}$+$\frac{{m}_{2}g}{{k}_{2}}$ | C. | $\frac{{m}_{1}g}{{k}_{1}}$+$\frac{{m}_{1}g}{{k}_{2}}$ | D. | $\frac{{(m}_{1}{+m}_{2})g}{{k}_{1}}$ |
 在“利用单摆测重力加速度g”的实验中:
在“利用单摆测重力加速度g”的实验中:(1)以下操作正确的是A.
A.要保证摆球始终在同一竖直面内摆动
B.为了便于计时观察,单摆的摆角应尽量大一些
C.测量摆长时,用刻度尺量出从悬点到摆球下端点间的距离
D.测量周期时从摆球通过平衡位置处时开始计时,当摆球再次通过平衡位置处时结束计时,秒表读数表示单摆的周期
(2)下表是一同学在实验中测得的数据:
| 组次 | 1 | 2 | 3 | 4 | 5 | 6 |
| 摆长l/m | 0.500 | 0.600 | 0.700 | 0.800 | 1.000 | 1.200 |
| 周期平方T2/s2 | 2.02 | 2.40 | 2.80 | 3.22 | 4.60 | 4.80 |
②利用图象,求出当地重力加速度值g为9.86m/s2.(π2=9.86,结果保留三位有效数字)
 一质量为1kg的质点静止于光滑水平面上,从t=0时刻开始,受到水平外力F作用,如图所示.下列判断正确的是( )
一质量为1kg的质点静止于光滑水平面上,从t=0时刻开始,受到水平外力F作用,如图所示.下列判断正确的是( )| A. | 0~2 s内外力的平均功率是4 W | |
| B. | 第2 s内外力所做的功是4 J | |
| C. | 第2 s末外力的瞬时功率最大 | |
| D. | 第1 s末与第2 s末外力的瞬时功率之比为9:5 |

