��Ŀ����
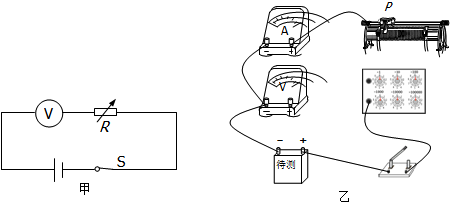
19������Ϊijͬѧ�õ��ڲ������ص��������ٶ�ʵ�鲿�ֲ�������1��Ϊ�˱Ƚ�ȷ�ز��������ص��������ٶ�ֵ��Ӧѡ���������������е���Щ������ѡ�õ����ĵ���ĸ�������ĺ����ϣ�
A����1m���ҵ�ϸ��
B����30m���ҵ�ϸ��
C��ֱ��2cm��Ǧ��
D��ֱ��2cm��ľ��
E�����
F��ʱ��
G����С�̶��Ǻ��Ŀ̶ȳ�
H����С�̶������Ŀ̶ȳ�
��ѡ���������ACEG��
��2�����α꿨�߲���С����ֱ����������ͼ1��ʾ������Ϊ20.30mm��

��3���������ƫ��С��5��ʱ���n��ȫ��ʱ��Ϊt���ú��̶ȳ߲�ð��߳�ΪL���α꿨�߲�ð���ֱ��Ϊd����������õ���д�������������ٶȵ�һ�����ʽ��g=$\frac{4{��}^{2}{n}^{2}��L+\frac{d}{2}��}{{t}^{2}}$
��4����ͬѧ�����ͬ�ڳ�ʱ��Ӧ������T������T2-Lͼ�ߣ���ͼ2��ʾ��������ͼ����������A��B�����꣨x1��y1������x2��y2���������g=$\frac{4{��}^{2}��{x}_{2}-{x}_{1}��}{{y}_{2}-{y}_{1}}$
����ͬѧ��ڳ�ʱ©����С��뾶�����������������������Ҳ������ʵ������������T2-Lͼ�߷���õ�gֵ����ʵֵ����Dz���ģ�ѡ�ƫ����ƫС�����䡱����
���� ��1������ʵ��ԭ����ʵ��������ʵ��ע������ѡ��ʵ�����ģ�
��2���α꿨�ߵĶ����������߶��������α���������������
��3�����ݵ��ڵ����ڹ�ʽ�ó��������ٶȵı���ʽ��
��4�����ݵ��ڵ����ڹ�ʽ�ó�T2-L�ı���ʽ�����ͼ�ߵ�б������������ٶȣ�
��� �⣺��1���õ��ڲ��������ٶ�ʵ�飬Ϊ��Сʵ��������Ӧѡ��A����1m���ҵ�ϸ�ߣ�
ʵ��ʱӦʹ�����������С�����ܶȴ�İ��ʰ���Ӧѡ��C��ֱ��2cm���ҵ�Ǧ��
ʵ����Ҫ������ڵ����ڣ������Ҫѡ��E�������
��ڳ�ʱΪ��Сʵ����Ӧѡ��G����С�̶���mm�Ŀ̶ȳߣ�
��ѡ��ACEG��
��2���α꿨�ߵ����߶���Ϊ20mm���α����Ϊ0.05��6mm=0.30mm�������ն���Ϊ20.30mm��
��3������$T=2��\sqrt{\frac{l}{g}}$���g=$\frac{4{��}^{2}l}{{T}^{2}}$=$\frac{4{��}^{2}{n}^{2}��L+\frac{d}{2}��}{{t}^{2}}$��
��4������$T=2��\sqrt{\frac{l}{g}}$�ã�${T}^{2}=\frac{4{��}^{2}l}{g}$��ͼ�ߵ�б��k=$\frac{4{��}^{2}}{g}$=$\frac{{y}_{2}-{y}_{1}}{{x}_{2}-{x}_{1}}$����g=$\frac{4{��}^{2}}{k}$=$\frac{4{��}^{2}��{x}_{2}-{x}_{1}��}{{y}_{2}-{y}_{1}}$��
����ͬѧ��ڳ�ʱ©����С��뾶�����������������������Ҳ������ʵ������T2-Lͼ�ߵ�б�ʱ��ֲ��䣬����ͼ�������gֵ����ʵֵ��Ȳ��䣮
�ʴ�Ϊ����1��ACEG����2��20.30����3��$\frac{4{��}^{2}{n}^{2}��L+\frac{d}{2}��}{{t}^{2}}$����4��$\frac{4{��}^{2}��{x}_{2}-{x}_{1}��}{{y}_{2}-{y}_{1}}$�����䣮
���� ���ڰڳ��������ߵij��������뾶֮�ͣ������߳��������뾶֮�ͣ������״��㣻ͼ����ʵ�������dz��õķ�����Ҫ����ʵ�����ݵ�ͼ����������

| A�� | �������ת����ΪT=2��$\sqrt{\frac{mR}{��N}}$ | |
| B�� | �������ת����ΪT=��$\sqrt{\frac{mR}{��N}}$ | |
| C�� | ����ͬ�����ǵĹ���뾶Ϊ${��\frac{mg}{��N}��}^{\frac{1}{3}}$R | |
| D�� | ����ͬ�����ǵĹ���뾶Ϊ2${��\frac{mg}{��N}��}^{\frac{1}{3}}$R |

| A�� | Ǧ���ڵ�10��ľ�����˶�ʱ���ܴ����������ľ��һ���˶� | |
| B�� | Ǧ��ջ��ϵ�12��ľ�����ʱ���ٶȴ�СΪ$\sqrt{3}$m/s | |
| C�� | Ǧ���ڵ�12��ľ���ϻ���ʱ��12��ľ��ļ��ٶȴ�СΪ2m/s2 | |
| D�� | СǦ�������ܻ��ϲ�ͣ�ڵ�13��ľ���� |
 ��������ǿ��ʱ���ԡ���ī����Ϊ�����ķ������Ż��뿪����������ˮ�ķ�������Ѹ�ٵ��ˣ�����ǿ�����ң��ں�ˮ����Ӿ���ٶ�ͨ�����Դﵽÿ��15�����ϣ���ijһ��ֹ�ں�������Ϊ0.5kg���������������ʱ����0.06s�ڿ��Խ�����0.05kg��ˮ�֣��ԶԵ�108m/s���ٶ�ˮƽ��ǰ�����������������Ľṹʹˮ���������Բ��ƣ���
��������ǿ��ʱ���ԡ���ī����Ϊ�����ķ������Ż��뿪����������ˮ�ķ�������Ѹ�ٵ��ˣ�����ǿ�����ң��ں�ˮ����Ӿ���ٶ�ͨ�����Դﵽÿ��15�����ϣ���ijһ��ֹ�ں�������Ϊ0.5kg���������������ʱ����0.06s�ڿ��Խ�����0.05kg��ˮ�֣��ԶԵ�108m/s���ٶ�ˮƽ��ǰ�����������������Ľṹʹˮ���������Բ��ƣ���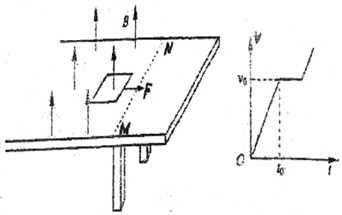

 ��ͼ��ʾ��һ����ͧͣ��ƽ����ˮ���ϣ�ͧǰ���϶���һ���P��������ǰ��A����һ���꣬���PA��������ֱ����ļн�Ϊ53�㣬DZˮԱ��DZ��ˮ��B��ʱ������P�պñ����굲ס����ǡ�ÿ���ͧβ�˺�ˮ���ϵľ����֪ˮ��������n=$\frac{4}{3}$��B�㵽ͧβ����ˮƽ����L=6m�����Ծ���ͧ�ij�ˮ��ȣ�
��ͼ��ʾ��һ����ͧͣ��ƽ����ˮ���ϣ�ͧǰ���϶���һ���P��������ǰ��A����һ���꣬���PA��������ֱ����ļн�Ϊ53�㣬DZˮԱ��DZ��ˮ��B��ʱ������P�պñ����굲ס����ǡ�ÿ���ͧβ�˺�ˮ���ϵľ����֪ˮ��������n=$\frac{4}{3}$��B�㵽ͧβ����ˮƽ����L=6m�����Ծ���ͧ�ij�ˮ��ȣ�