题目内容
9. 在垂直纸面向里的匀强磁场里,有一个与磁场方向垂直的边长为100 cm的正方形线圈,位置如图所示,如果穿过此线圈所未面积的磁通量为2.0×10-4Wb.求:
在垂直纸面向里的匀强磁场里,有一个与磁场方向垂直的边长为100 cm的正方形线圈,位置如图所示,如果穿过此线圈所未面积的磁通量为2.0×10-4Wb.求:(1)磁感应强度B的大小;
(2)若线圈由图示位置以角速度π rad/s匀速转过$\frac{π}{2}$,求此过程中线圈产生的平均感应电动势大小.
分析 (1)根据∅=BS求得磁感应强度;
(2)根据$\overline{E}=\frac{△∅}{△t}$求得平均感应电动势;
解答 解:(1)根据∅=BS可知B=$\frac{∅}{S}=\frac{0.0002}{0.1×0.1}T=0.02T$
(2)转过$\frac{π}{2}$所需时间t=$\frac{\frac{π}{2}}{π}=\frac{1}{2}$s,产生的平均感应电动势$\overline{E}=\frac{BS}{t}=\frac{2×1{0}^{-4}}{0.5}V=4×1{0}^{-4}V$
答:(1)磁感应强度B的大小为0.02T;
(2)若线圈由图示位置以角速度π rad/s匀速转过$\frac{π}{2}$,此过程中线圈产生的平均感应电动势大小为4×10-4V.
点评 本题考查了磁通量的定义式和公式Φ=BS的适用范围,只要掌握了磁通量的定义和公式Φ=BS的适用条件就能顺利解决.

练习册系列答案
 期末集结号系列答案
期末集结号系列答案
相关题目
18.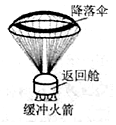 如图,“神州”系列航天飞船返回舱返回地面的示意图,其过程可简化为:打开降落伞一段时间后,整个装置匀速下降,为确保安全着陆,需点燃返回舱的缓冲火箭,在火箭喷气过程中返回舱做减速直线运动,则( )
如图,“神州”系列航天飞船返回舱返回地面的示意图,其过程可简化为:打开降落伞一段时间后,整个装置匀速下降,为确保安全着陆,需点燃返回舱的缓冲火箭,在火箭喷气过程中返回舱做减速直线运动,则( )
 如图,“神州”系列航天飞船返回舱返回地面的示意图,其过程可简化为:打开降落伞一段时间后,整个装置匀速下降,为确保安全着陆,需点燃返回舱的缓冲火箭,在火箭喷气过程中返回舱做减速直线运动,则( )
如图,“神州”系列航天飞船返回舱返回地面的示意图,其过程可简化为:打开降落伞一段时间后,整个装置匀速下降,为确保安全着陆,需点燃返回舱的缓冲火箭,在火箭喷气过程中返回舱做减速直线运动,则( )| A. | 返回舱在喷气过程中处于失重状态 | |
| B. | 返回舱在喷气过程中减速的主要原因是空气阻力 | |
| C. | 返回舱在喷气过程中所受合外力可能做正功 | |
| D. | 火箭开始喷气瞬间伞绳对返回舱的拉力变小 |
14. 如图,质量为m的小球从斜轨道高h处由静止滑下,然后沿竖直圆轨道的内侧运动,已知圆轨道的半径为R,不计一切摩擦阻力,重力加速度为g,则下列说法正确的是( )
如图,质量为m的小球从斜轨道高h处由静止滑下,然后沿竖直圆轨道的内侧运动,已知圆轨道的半径为R,不计一切摩擦阻力,重力加速度为g,则下列说法正确的是( )
 如图,质量为m的小球从斜轨道高h处由静止滑下,然后沿竖直圆轨道的内侧运动,已知圆轨道的半径为R,不计一切摩擦阻力,重力加速度为g,则下列说法正确的是( )
如图,质量为m的小球从斜轨道高h处由静止滑下,然后沿竖直圆轨道的内侧运动,已知圆轨道的半径为R,不计一切摩擦阻力,重力加速度为g,则下列说法正确的是( )| A. | 当h≤R时,小球在运动过程中不会脱离轨道 | |
| B. | 当h=R时,小球在最低点N时对轨道压力为2mg | |
| C. | 当h=2R时,小球恰好能到达最高点M | |
| D. | 当h=2R时,小球在圆心等高处P时对轨道压力为2mg |
1.用起重机将一个质量为m的货物竖直向上以加速度a匀加速提升H米,在这个过程中,以下说法中正确的是( )
| A. | 物体的重力势能增加了maH | B. | 机械能增加了m(g+a)H | ||
| C. | 物体的动能增加了maH | D. | 物体的机械能增加了mgH |
18.一个物体从地面竖直上抛,到达最高点后又落回抛出点,若上升和下降过程中物体所受空气阻力大小恒定,则( )
| A. | 物体下落过程的加速度大于上升过程的加速度 | |
| B. | 物体下落过程所用的时间大于上升过程所用的时间 | |
| C. | 物体下落过程中的平均速度大于上升过程中的平均速度 | |
| D. | 物体下落到抛出点的速率与抛出时的速率相等 |
15.如图甲所示,在距离水平地面高度为0.8m的平台上有一轻质弹簧,其左端固定于竖直挡板上,右端与质量为0.2kg的物块(可看做质点)相接触(不粘连),平台OA段粗糙且长度等于弹簧原长,其余位置均光滑.物块开始静止于A点,与OA段的动摩擦因数为0.4.现对物块施加一个水平向左的外力F,大小随位移x变化关系如图乙所示.物块向左运动0.2m到达B点,且到达B点时速度为零,随即撤去外力F,物块在弹簧弹力作用下向右运动,从M点离开平台,落到地面上N点,取g=10m/s2,弹簧始终在弹性限度内,则( )


| A. | 弹簧被压缩过程中外力F做的功为2.5J | |
| B. | 弹簧被压缩过程中具有的最大弹性势能为2.18J | |
| C. | 整个运动过程中克服摩擦力做功为0.32J | |
| D. | M、N两点的水平距离为2m |
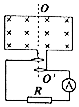 如图所示,N匝矩形导线框在磁感应强度为B的匀强磁场中绕轴OO′匀速转动,线框面积为S,线框的电阻、电感均不计,外电路接有电阻R、理想交流电流表A,电流表的示数为I,求;
如图所示,N匝矩形导线框在磁感应强度为B的匀强磁场中绕轴OO′匀速转动,线框面积为S,线框的电阻、电感均不计,外电路接有电阻R、理想交流电流表A,电流表的示数为I,求; 在如图所示的皮带传动装置中,a是小轮边缘上的一点,b是大轮边缘上的一点,两轮半径之比为2:3.当皮带轮匀速转动时,皮带与轮间不打滑.a、b两点的线速度之比为1:1,a、b两点的角速度之比为3:2.
在如图所示的皮带传动装置中,a是小轮边缘上的一点,b是大轮边缘上的一点,两轮半径之比为2:3.当皮带轮匀速转动时,皮带与轮间不打滑.a、b两点的线速度之比为1:1,a、b两点的角速度之比为3:2.