题目内容
2. 如图所示,在第一象限内有垂直纸面向里和向外的匀强磁场,磁感应强度分别为B1=0.2T、B2=0.05T,分界线OM与x轴正方向的夹角为α.在第二、三象限内存在着沿x轴正方向的匀强电场,电场强度E=1×104V/m.现有一带电粒子由x轴上A点静止释放,从O点进入匀强磁场区域.已知A点横坐标xA=-5×10-2m,带电粒子的质量m=1.6×10-24kg,电荷量q=+1.6×10-15C.
如图所示,在第一象限内有垂直纸面向里和向外的匀强磁场,磁感应强度分别为B1=0.2T、B2=0.05T,分界线OM与x轴正方向的夹角为α.在第二、三象限内存在着沿x轴正方向的匀强电场,电场强度E=1×104V/m.现有一带电粒子由x轴上A点静止释放,从O点进入匀强磁场区域.已知A点横坐标xA=-5×10-2m,带电粒子的质量m=1.6×10-24kg,电荷量q=+1.6×10-15C.(1)如果α=30o,在OM上有一点P,OP=3×10-2m,粒子从进入O点计时,经多长时间经过P点?
(2)要使带电粒子能始终在第一象限内运动,求α的取值范围?(已知sin37°=0.6,cos37°=0.8)
分析 (1)粒子在电场中做初速度为零的匀加速直线运动,根据动能定理列式求解末速度;进入磁场后,做匀速圆周运动,洛仑兹力提供向心力,根据牛顿第二定律列式求解轨道半径,画出运动轨迹,注意粒子通过直线边界时,进入时速度与边界线的夹角等于离开时速度与边界线的夹角;
(2)正确画出轨迹,由几何知识及三角函数求解.
解答 解:(1)在电场中加速过程,根据动能定理,有:$qE{x_A}=\frac{1}{2}m{v^2}$,
解得:v=$\sqrt{\frac{2qE{x}_{A}}{m}}$=$\sqrt{\frac{2×1.6×1{0}^{-15}×1×1{0}^{4}×5×1{0}^{-2}}{1.6×1{0}^{-24}}}$m/s=1×106m/s;
粒子在磁场中运动时,根据牛顿第二定律,有:$qvB=m\frac{v^2}{r}$,
解得:r=$\frac{mv}{qB}$;
故${r_1}=\frac{mv}{{q{B_1}}}=\frac{{1.6×1{0^{-24}}kg×{{10}^6}m/s}}{{1.6×1{0^{-15}}C×0.2T}}=5×{10^{-3}}m$
${r_2}=\frac{mv}{{q{B_2}}}=\frac{{1.6×1{0^{-24}}kg×{{10}^6}m/s}}{{1.6×1{0^{-15}}C×0.05T}}=2×{10^{-2}}m$
粒子通过直线边界OM时,进入时速度与边界线的夹角等于离开时速度与边界线的夹角,故经过B1磁场时沿着OM前进r1距离,经过B2磁场时沿着OM前进r2距离,由于OP=3×10-2m=2r1+r2,故轨迹如图所示:
故粒子从进入O点计时,到达P点经过的时间为:
t=$\frac{60°+60°}{360°}{T}_{1}+\frac{60°}{360°}{T}_{2}$=$\frac{1}{3}×\frac{2πm}{q{B}_{1}}+\frac{1}{6}×\frac{2πm}{q{B}_{2}}$=$\frac{{2π×1.6×1{0^{-24}}}}{{3×1.6×1{0^{-15}}×0.2}}+\frac{{π×1.6×1{0^{-24}}}}{{3×1.6×1{0^{-15}}×0.05}}$=3.14×10-8s
(2)由于 r2=2r1,画出临界轨迹,如图所示: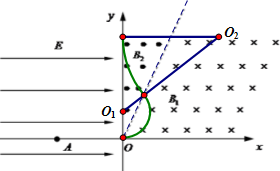
由几何关系解得:cosα=$\frac{{r}_{2}}{{r}_{1}+{r}_{2}}$=$\frac{2}{3}$,故α≤arccos$\frac{2}{3}$=48.2°;
答:(1)如果α=30o,在OM上有一点P,OP=3×10-2m,粒子从进入O点计时,经3.14×10-8s时间经过P点;
(2)要使带电粒子能始终在第一象限内运动,α的取值范围为α≤48.2°.
点评 此题考查了粒子在复合场中的运动,需考生熟练掌握圆周运动的公式及应用.首先根据题意,画出粒子的运动轨迹,找到临界值,求出角度.根据草图找出粒子经过哪些点,通过分析得出数学规律.

 一个劲度系数为k,绝缘材料制成的轻弹簧,一端固定,另一端与质量为m,带正电荷q的小球相连,静止在光滑绝缘水平面上,当加入如图所示的场强为E的匀强电场后,小球开始运动,下列说法正确的是( )
一个劲度系数为k,绝缘材料制成的轻弹簧,一端固定,另一端与质量为m,带正电荷q的小球相连,静止在光滑绝缘水平面上,当加入如图所示的场强为E的匀强电场后,小球开始运动,下列说法正确的是( )| A. | 球的速度为零时,弹簧伸长$\frac{Eq}{k}$ | |
| B. | 球做简谐振动,振幅为$\frac{2Eq}{k}$ | |
| C. | 运动过程中,小球的机械能守恒 | |
| D. | 运动过程中,是电势能、动能和弹性势能相互转化 |
 如图所示电路中,A1和A2为理想电流表,示数分别为I1和I2,R1:R2:R3=1:2:3.当a、b两点间加以恒定的电压U后,下列结论正确的是( )
如图所示电路中,A1和A2为理想电流表,示数分别为I1和I2,R1:R2:R3=1:2:3.当a、b两点间加以恒定的电压U后,下列结论正确的是( )| A. | I1:I2=3:4 | |
| B. | I1:I2=9:5 | |
| C. | 将A1、A2换理想电压表,其示数之比为3:5 | |
| D. | 将A1、A2换理想电压表,其示数之比为1:1 |

 如图所示,在x≥O的区域内存在与xOy平面垂直的匀强磁场,磁感应强度的大小为B,方向垂直于纸面朝里,假设一系列质量为m、电荷量为q的正离子初速度为零,经过加速电场加速后从O点沿Ox轴正方向进入匀强磁场区域.有一块厚度不计、高度为d的金属板竖直放置在磁场中,截面如图,M、N分别为金属板截面的上、下端点,M点的坐标为(d,2d),N点的坐标为(d,d).不计正离子的重力.
如图所示,在x≥O的区域内存在与xOy平面垂直的匀强磁场,磁感应强度的大小为B,方向垂直于纸面朝里,假设一系列质量为m、电荷量为q的正离子初速度为零,经过加速电场加速后从O点沿Ox轴正方向进入匀强磁场区域.有一块厚度不计、高度为d的金属板竖直放置在磁场中,截面如图,M、N分别为金属板截面的上、下端点,M点的坐标为(d,2d),N点的坐标为(d,d).不计正离子的重力. 如图所示,在半径为b(大小未知)的圆形区域内,固定放置一绝缘材料制成的边长为L的弹性等边三角形框架DEF,其中心O位于磁场区域的圆心.在三角形框架DEF与圆周之间的空间中,充满磁感应强度大小为B的均匀磁场,其方向垂直纸面向里.在三角形DEF内平行于EF边有一个粒子加速器MN,d,N板紧靠EF边,N板及EF中点S处均开有小孔,在两板间靠近M板处有一质量为m电量为q(q>0)的带电粒子静止释放,粒子经过S处的速度大小为v=$\frac{qBL}{2m}$,方向垂直于EF边并指向磁场,若粒子与三角形框架的碰撞均为弹性碰撞,且粒子在碰撞过程中质量、电量均不变.(不计带电粒子的重力,不计带电粒子之间的相互作用)求:
如图所示,在半径为b(大小未知)的圆形区域内,固定放置一绝缘材料制成的边长为L的弹性等边三角形框架DEF,其中心O位于磁场区域的圆心.在三角形框架DEF与圆周之间的空间中,充满磁感应强度大小为B的均匀磁场,其方向垂直纸面向里.在三角形DEF内平行于EF边有一个粒子加速器MN,d,N板紧靠EF边,N板及EF中点S处均开有小孔,在两板间靠近M板处有一质量为m电量为q(q>0)的带电粒子静止释放,粒子经过S处的速度大小为v=$\frac{qBL}{2m}$,方向垂直于EF边并指向磁场,若粒子与三角形框架的碰撞均为弹性碰撞,且粒子在碰撞过程中质量、电量均不变.(不计带电粒子的重力,不计带电粒子之间的相互作用)求: 匀强电场中有M、N、P三点,连成一个直角三角形,MN=4cm,MP=5cm,如图8所示,把一个电量为-2×10-9C的检验电荷从M点移到N点,电场力做功8×10-9J,从M点移到P点电场力做功也是8×10-9J.则匀强电场的方向为N指向M?电场强度大小为100V/m?
匀强电场中有M、N、P三点,连成一个直角三角形,MN=4cm,MP=5cm,如图8所示,把一个电量为-2×10-9C的检验电荷从M点移到N点,电场力做功8×10-9J,从M点移到P点电场力做功也是8×10-9J.则匀强电场的方向为N指向M?电场强度大小为100V/m? 如图所示,电灯的重力为20N,绳OA与天花板间的夹角为45°.绳OB水平,求绳OA、OB所受的拉力?
如图所示,电灯的重力为20N,绳OA与天花板间的夹角为45°.绳OB水平,求绳OA、OB所受的拉力?