题目内容
13. 在倾角为θ的固定光滑斜面上有两个用轻弹簧相连接的物块A、B,它们的质量均为m,弹簧劲度系数为k,C为一固定挡板,系统处于静止状态.现用一平行于斜面向上的恒力F拉物块A使之向上运动,直到物块A达到最大速度v,此时物块B刚要离开挡板C.重力加速度为g,则( )
在倾角为θ的固定光滑斜面上有两个用轻弹簧相连接的物块A、B,它们的质量均为m,弹簧劲度系数为k,C为一固定挡板,系统处于静止状态.现用一平行于斜面向上的恒力F拉物块A使之向上运动,直到物块A达到最大速度v,此时物块B刚要离开挡板C.重力加速度为g,则( )| A. | 在此过程中,物块A的位移为$\frac{2mgsinθ}{k}$ | |
| B. | 在此过程中,物块A的机械能增加量为$\frac{2{m}^{2}{g}^{2}si{n}^{2}θ}{k}$+$\frac{1}{2}$mv2 | |
| C. | 在此过程中,弹簧的弹性势能增加量为$\frac{2{m}^{2}{g}^{2}si{n}^{2}θ}{k}$ | |
| D. | 物块B刚要离开挡板C时,突然撤去恒力F,物块A的加速度等于$\frac{F-mgsinθ}{m}$ |
分析 开始时,弹簧的弹力等于A的重力沿斜面下的分力,由胡克定律求出弹簧的压缩量.当B刚要离开C时,弹簧的弹力等于B的重力沿斜面下的分力,根据胡克定律求解出弹簧的伸长量,从而得到物块A的位移;求F做的功,根据机械能的概念可求物块A的机械能增加量.根据形变量的关系分析弹簧弹性势能的增加量.根据牛顿第二定律求A的加速度.
解答 解:A、开始时系统处于静止状态,弹簧的弹力等于A的重力沿斜面向下的分力,则有 mgsinθ=kx1.当B刚要离开C时,弹簧的弹力等于B的重力沿斜面下的分力,故mgsinθ=kx2.在此过程中,物块A的位移为 s=x1+x2=$\frac{2mgsinθ}{k}$,故A正确.
B、在此过程中,物块A的机械能增加量等于重力势能的增加量与动能的增加量之和,为mgsinθ•s+$\frac{1}{2}m{v}^{2}$=$\frac{2{m}^{2}{g}^{2}si{n}^{2}θ}{k}$+$\frac{1}{2}$mv2.故B正确.
C、由于x1=x2,所以弹簧的弹性势能增加量为零,故C错误.
D、物块B刚要离开挡板C时,突然撤去恒力F,对物块A,有 mgsinθ+kx2=ma,得 a=2gsinθ.
物块A达到最大速度时,合力等于零,则有 F=mgsinθ+kx2=2mgsinθ,可知 a=2$\frac{F-mgsinθ}{m}$,故D错误.
故选:AB
点评 含有弹簧的问题,往往要研究弹簧的状态,分析物块的位移与弹簧压缩量和伸长量的关系是常用思路.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
1.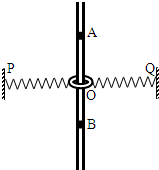 如图所示,一质量为m的刚性圆环套在固定细杆上,圆环的直径略大于细杆的直径,圆环的两边与两个相同的轻质弹簧的一端相连,轻质弹簧的另一端连在和圆环同一高度的墙壁上的P、Q两点处,弹簧的劲度系数为k,起初圆环处于O点,弹簧处于原长状态且弹簧的原长为L,细杆上面的A、B两点到O点的距离都为L,将圆环拉至A点由静止释放,重力加速度为g,对于圆环从A点运动到B点的过程,下列说法正确的是( )
如图所示,一质量为m的刚性圆环套在固定细杆上,圆环的直径略大于细杆的直径,圆环的两边与两个相同的轻质弹簧的一端相连,轻质弹簧的另一端连在和圆环同一高度的墙壁上的P、Q两点处,弹簧的劲度系数为k,起初圆环处于O点,弹簧处于原长状态且弹簧的原长为L,细杆上面的A、B两点到O点的距离都为L,将圆环拉至A点由静止释放,重力加速度为g,对于圆环从A点运动到B点的过程,下列说法正确的是( )
 如图所示,一质量为m的刚性圆环套在固定细杆上,圆环的直径略大于细杆的直径,圆环的两边与两个相同的轻质弹簧的一端相连,轻质弹簧的另一端连在和圆环同一高度的墙壁上的P、Q两点处,弹簧的劲度系数为k,起初圆环处于O点,弹簧处于原长状态且弹簧的原长为L,细杆上面的A、B两点到O点的距离都为L,将圆环拉至A点由静止释放,重力加速度为g,对于圆环从A点运动到B点的过程,下列说法正确的是( )
如图所示,一质量为m的刚性圆环套在固定细杆上,圆环的直径略大于细杆的直径,圆环的两边与两个相同的轻质弹簧的一端相连,轻质弹簧的另一端连在和圆环同一高度的墙壁上的P、Q两点处,弹簧的劲度系数为k,起初圆环处于O点,弹簧处于原长状态且弹簧的原长为L,细杆上面的A、B两点到O点的距离都为L,将圆环拉至A点由静止释放,重力加速度为g,对于圆环从A点运动到B点的过程,下列说法正确的是( )| A. | 圆环通过O点的加速度等于g | |
| B. | 圆环在O点的速度最大 | |
| C. | 圆环在A点时的加速度大小为g+$\frac{(2-\sqrt{2})kL}{m}$ | |
| D. | 圆环在B点的速度为2$\sqrt{gL}$ |
5.2016年元旦节间人们燃放起美丽的焰火以庆祝新的一年国泰平安、阖家欢乐,射洪县某烟花厂生产的某种型号的装有焰火的礼花弹从专用炮筒中射出后,在4s末到达离地面100m的最高点时炸开,构成各种美丽的图案.假设礼花弹从炮筒中竖直向上射出时的初速度是v0,上升过程中所受的阻力大小始终是自身重力的k倍,g=10m/s2,那么v0和k分别等于( )
| A. | 100m/s,0.25 | B. | 100m/s,0.5 | C. | 50m/s,0.25 | D. | 50m/s,0.5 |
3. 如图所示,固定的竖直光滑长杆上套有质量为m的小圆环,圆环与水平状态的轻质弹簧一端连接,弹簧的另一端连接在墙上,并且处于原长状态.现让圆环由静止开始下滑,已知弹簧原长为L,圆环下滑到最大距离时弹簧的长度变为2L(未超过弹性限度),则在圆环下滑到最大距离的过程中( )
如图所示,固定的竖直光滑长杆上套有质量为m的小圆环,圆环与水平状态的轻质弹簧一端连接,弹簧的另一端连接在墙上,并且处于原长状态.现让圆环由静止开始下滑,已知弹簧原长为L,圆环下滑到最大距离时弹簧的长度变为2L(未超过弹性限度),则在圆环下滑到最大距离的过程中( )
 如图所示,固定的竖直光滑长杆上套有质量为m的小圆环,圆环与水平状态的轻质弹簧一端连接,弹簧的另一端连接在墙上,并且处于原长状态.现让圆环由静止开始下滑,已知弹簧原长为L,圆环下滑到最大距离时弹簧的长度变为2L(未超过弹性限度),则在圆环下滑到最大距离的过程中( )
如图所示,固定的竖直光滑长杆上套有质量为m的小圆环,圆环与水平状态的轻质弹簧一端连接,弹簧的另一端连接在墙上,并且处于原长状态.现让圆环由静止开始下滑,已知弹簧原长为L,圆环下滑到最大距离时弹簧的长度变为2L(未超过弹性限度),则在圆环下滑到最大距离的过程中( )| A. | 圆环机械能与弹簧弹性势能之和保持不变 | |
| B. | 圆环下滑到最大距离时,所受合力为零 | |
| C. | 圆环下滑到最大距离时,弹簧弹性势能变化了$\sqrt{3}$mgL | |
| D. | 圆环的加速度逐渐减小 |

 电饭锅工作时有两种状态:一种是锅内的水烧干以前的加热状态,另一种是水烧干以后的保温状态.如图所示是电饭锅的电路图,R1是电阻,R2是加热用的电热丝,S是自动开关.开关S接通时,电饭锅处于加热状态.(填“保温”或“加热”)当R1:R2=1:1时,R2在保温状态下的功率与在加热状态下的功率比值是1:4.
电饭锅工作时有两种状态:一种是锅内的水烧干以前的加热状态,另一种是水烧干以后的保温状态.如图所示是电饭锅的电路图,R1是电阻,R2是加热用的电热丝,S是自动开关.开关S接通时,电饭锅处于加热状态.(填“保温”或“加热”)当R1:R2=1:1时,R2在保温状态下的功率与在加热状态下的功率比值是1:4. 如图所示,水平轨道BC的左端与固定的光滑竖直半圆轨道相切于C点,右端与一倾角为30°的光滑斜面轨道在B点平滑连接(即物体经过B点时速度的大小不变),斜面顶端固定一轻质弹簧,一质量为m=1kg的滑块压缩弹簧至A点,现将滑块由静止释放,滑块滑上半圆轨道后恰好能通过半圆轨道的最高点E.已知,光滑斜面轨道上AB长为s1=0.6m,水平轨道BC长为s2=0.4m,其动摩擦因数μ=0.2,光滑圆轨道的半径R=0.45m,g取10m/s2,求:
如图所示,水平轨道BC的左端与固定的光滑竖直半圆轨道相切于C点,右端与一倾角为30°的光滑斜面轨道在B点平滑连接(即物体经过B点时速度的大小不变),斜面顶端固定一轻质弹簧,一质量为m=1kg的滑块压缩弹簧至A点,现将滑块由静止释放,滑块滑上半圆轨道后恰好能通过半圆轨道的最高点E.已知,光滑斜面轨道上AB长为s1=0.6m,水平轨道BC长为s2=0.4m,其动摩擦因数μ=0.2,光滑圆轨道的半径R=0.45m,g取10m/s2,求: