题目内容
1. 如图所示,人骑摩托车做腾跃特技表演,沿半径为3.2m的$\frac{1}{4}$圆弧桥面运动,到桥面最高点时汽车对桥面的压力为1224N,然后水平飞出落到与圆心同高的水平面,已知人和车的总质量为180kg,特技表演的全程中不计一切阻力,取g=10m/s2.则:
如图所示,人骑摩托车做腾跃特技表演,沿半径为3.2m的$\frac{1}{4}$圆弧桥面运动,到桥面最高点时汽车对桥面的压力为1224N,然后水平飞出落到与圆心同高的水平面,已知人和车的总质量为180kg,特技表演的全程中不计一切阻力,取g=10m/s2.则:(1)求人和车到达顶部平台时的速度v0;
(2)求人和车从桥面飞出的水平距离L.
分析 (1)根据牛顿第二定律,结合竖直方向的合力提供向心力求出人和车到达顶部平台的速度.
(2)根据高度求出平抛运动的时间,结合初速度和时间求出水平距离.
解答 解:(1)在最高点,根据牛顿第二定律得,$mg-N=m\frac{{{v}_{0}}^{2}}{R}$,
代入数据解得v0=3.2m/s.
(2)根据$R=\frac{1}{2}g{t}^{2}$得,t=$\sqrt{\frac{2R}{g}}=\sqrt{\frac{2×3.2}{10}}s=0.8s$,
则人和车从桥面飞出的水平距离L=v0t=3.2×0.8m=2.56m.
答:(1)人和车到达顶部平台的速度为 3.2m/s;
(2)人和车从桥面飞出的水平距离为2.56m.
点评 本题考查了平抛运动和圆周运动的综合运用,知道平抛运动在水平方向和竖直方向上的运动规律以及圆周运动向心力的来源是解决本题的关键.

练习册系列答案
相关题目
7.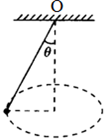 如图所示,长为L的细线拴一个质量为M的小球,使小球在水平面内做匀速圆周运动,细线与竖直方向的夹角为θ,关于小球的受力情况,下列说法正确的是( )
如图所示,长为L的细线拴一个质量为M的小球,使小球在水平面内做匀速圆周运动,细线与竖直方向的夹角为θ,关于小球的受力情况,下列说法正确的是( )
 如图所示,长为L的细线拴一个质量为M的小球,使小球在水平面内做匀速圆周运动,细线与竖直方向的夹角为θ,关于小球的受力情况,下列说法正确的是( )
如图所示,长为L的细线拴一个质量为M的小球,使小球在水平面内做匀速圆周运动,细线与竖直方向的夹角为θ,关于小球的受力情况,下列说法正确的是( )| A. | 小球受到重力、线的拉力和向心力三个力 | |
| B. | 向心力由细绳拉力与重力的合力提供 | |
| C. | 向心力的方向指向悬挂点O | |
| D. | 向心力的大小等于$\frac{Mg}{cosθ}$ |
4.下列说法错误的是( )
| A. | 开普勒确切描述了行星的运动 | B. | 牛顿发现了万有引力定律 | ||
| C. | 卡文迪许测出了引力常量 | D. | 阿基米德被称为称出地球质量的人 |
5.从同一点水平抛出三个小球分别撞在竖直墙壁上a点、b点、c点,则( )


| A. | 落在a点的小球水平速度最小 | |
| B. | 落在b点的小球竖直速度最小 | |
| C. | 落在c点的小球飞行时间最短 | |
| D. | a、b、c三点速度方向的反向延长线交于一点 |
 在如图所示的电路中,电源电动势是4.5V、内阻是0.5Ω,电阻R1=4Ω,R2=4.5Ω.
在如图所示的电路中,电源电动势是4.5V、内阻是0.5Ω,电阻R1=4Ω,R2=4.5Ω. 如图,两个弹性小球a和b的质量分别为ma、mb.a球原来静止在离地高度H=2.4m的P点,b球原来静止在离地高度h=1.6m的Q点,先静止释放a球,在a球即将碰到b球时同样静止释放b球,两球碰撞时间极短,碰后在同一竖直线运动,己知mb=3ma,重力加速度大小g=10m/s2,忽略小球大小、空气阻力及碰撞中的动能损失,且小球落地后不再跳起,求:
如图,两个弹性小球a和b的质量分别为ma、mb.a球原来静止在离地高度H=2.4m的P点,b球原来静止在离地高度h=1.6m的Q点,先静止释放a球,在a球即将碰到b球时同样静止释放b球,两球碰撞时间极短,碰后在同一竖直线运动,己知mb=3ma,重力加速度大小g=10m/s2,忽略小球大小、空气阻力及碰撞中的动能损失,且小球落地后不再跳起,求: 如图甲所示,在半径为R的圆往形区域内存在方向竖直向上的匀强磁场,根据麦克斯韦电磁理论,当磁场均匀增加时,会在空间激发恒定的感生电场,其电场线是在水平面内一系列沿顺时针方向的同心圆,圆心与磁场区域的中心O重合.在半径为r的圆周上,感生电场的电场强度大小处处相等,并且可以用E=$\frac{?}{2πr}$计算,式中?为由于磁场均匀变化而在半径为r的圆周上产生的感生电动势.
如图甲所示,在半径为R的圆往形区域内存在方向竖直向上的匀强磁场,根据麦克斯韦电磁理论,当磁场均匀增加时,会在空间激发恒定的感生电场,其电场线是在水平面内一系列沿顺时针方向的同心圆,圆心与磁场区域的中心O重合.在半径为r的圆周上,感生电场的电场强度大小处处相等,并且可以用E=$\frac{?}{2πr}$计算,式中?为由于磁场均匀变化而在半径为r的圆周上产生的感生电动势. 如图所示,光滑水平面上有一个质量为M=4kg的内有光滑半圆槽轨道的滑块B,半圆槽的半径R=0.4m,今让一小球自半圆槽轨道右端正上方高h=0.8m处的A点自由落下,已知小球(可看成质点)的质量m=2kg,g=10m/s2,求小球滑到半圆槽最低点的速度大小及此时B的速度大小.
如图所示,光滑水平面上有一个质量为M=4kg的内有光滑半圆槽轨道的滑块B,半圆槽的半径R=0.4m,今让一小球自半圆槽轨道右端正上方高h=0.8m处的A点自由落下,已知小球(可看成质点)的质量m=2kg,g=10m/s2,求小球滑到半圆槽最低点的速度大小及此时B的速度大小.