题目内容
20. 细杆的一端与小球相连,可绕O点的水平轴自由转动,不计摩擦,杆长为R.
细杆的一端与小球相连,可绕O点的水平轴自由转动,不计摩擦,杆长为R.(1)若球在最高点速度为$\frac{\sqrt{gR}}{2}$时,杆对球作用力为多少?
(2)若球在最高点速度为2$\sqrt{gR}$时,杆对球作用力为多少?
分析 对小球进行受力分析,由于小球做圆周运动,小球需要向心力.找出小球向心力的来源,根据牛顿第二定律列出等式,判断杆对球的作用力的方向.
解答 解:(1)当在最高点时对杆没有作用力时,重力提供向心力,得:$mg=\frac{m{v}_{0}^{2}}{R}$
所以:${v}_{0}=\sqrt{gR}$
若球在最高点速度为$\frac{\sqrt{gR}}{2}$时,$\frac{\sqrt{gR}}{2}<\sqrt{gR}$,杆对小球的作用力的方向向上,重力与支持力的合力提供向心力,得:
$mg-{N}_{1}=\frac{m{v}_{1}^{2}}{R}$
得:${N}_{1}=mg-\frac{m{v}_{1}^{2}}{R}=mg-\frac{m•\frac{gR}{4}}{R}=\frac{3}{4}mg$
(2)当在最高点时速度v>$\sqrt{gR}$时,小球的重力不足以提供向心力,轻杆对小球有指向圆心的拉力.
此时:$mg+{N}_{2}=\frac{m{v}_{2}^{2}}{R}$
故${N}_{2}=\frac{m{v}_{2}^{2}}{R}-mg=\frac{m•4gR}{R}-mg=3mg$
答:(1)若球在最高点速度为$\frac{\sqrt{gR}}{2}$时,杆对球作用力为$\frac{3}{4}mg$,方向向上;
(2)若球在最高点速度为2$\sqrt{gR}$时,杆对球作用力为3mg,方向向下.
点评 轻杆的作用力可以提供支持力,也可以提供拉力,
要判断是拉力还是支持力,我们要从小球所需要得向心力入手研究,根据需要的向心力的大小和方向确定杆子的作用力.

练习册系列答案
相关题目
15.将一个有确定方向的力F=20N分解成两个分力,下列说法错误的是( )
| A. | 已知一个分力有确定的方向,与F成30°夹角,另一个分力的大小为12N,则在分解时有两组解 | |
| B. | 已知一个分力有确定的方向,与F成30°夹角,则另一个分力的最小值为10N | |
| C. | 两个分力的大小可能是15N和25N | |
| D. | 两个分力的大小可能是8N和10N |
10. 如图所示,物体A、B用绕过光滑滑轮的轻绳连接,A放在水平桌面上被水平细绳拉着处于静止状态,A、B的质量分别为M、m,A与水平面之间的摩擦因数为μ(μ<1),则下列说法正确的是( )
如图所示,物体A、B用绕过光滑滑轮的轻绳连接,A放在水平桌面上被水平细绳拉着处于静止状态,A、B的质量分别为M、m,A与水平面之间的摩擦因数为μ(μ<1),则下列说法正确的是( )
 如图所示,物体A、B用绕过光滑滑轮的轻绳连接,A放在水平桌面上被水平细绳拉着处于静止状态,A、B的质量分别为M、m,A与水平面之间的摩擦因数为μ(μ<1),则下列说法正确的是( )
如图所示,物体A、B用绕过光滑滑轮的轻绳连接,A放在水平桌面上被水平细绳拉着处于静止状态,A、B的质量分别为M、m,A与水平面之间的摩擦因数为μ(μ<1),则下列说法正确的是( )| A. | 质量M大于质量m | B. | A对桌面的摩擦力方向水平向右 | ||
| C. | 绳子对A的拉力大于绳子对B的拉力 | D. | 绳子对A的拉力等于B的重力大小 |
 如图所示.半径分别为a、b的两同心虚线圆所围空间分别存在电场和磁场,中心O处固定一个半径很小(可忽略不计)的金属球,在小圆空间内存在沿半径向内的辐向电场,小圆周与金属球间电势差U,两圆之间存在垂直于纸面向里的匀强磁场,设有一个带负电的粒子从金属球表面沿x轴正方向以很小的初速度逸出,粒子质量为m,电荷量为q.(不计粒子的重力,忽略粒子逸出的初速度)试求:
如图所示.半径分别为a、b的两同心虚线圆所围空间分别存在电场和磁场,中心O处固定一个半径很小(可忽略不计)的金属球,在小圆空间内存在沿半径向内的辐向电场,小圆周与金属球间电势差U,两圆之间存在垂直于纸面向里的匀强磁场,设有一个带负电的粒子从金属球表面沿x轴正方向以很小的初速度逸出,粒子质量为m,电荷量为q.(不计粒子的重力,忽略粒子逸出的初速度)试求: 如图所示,质量m=20kg的物体以水平速度v0=5m/s滑到静止在光滑水平地面的平板小车上.小车质量M=80kg,物体在小车上滑行一段距离后相对于小车静止.已知物体与平板间的动摩擦因数μ=0.8,g取10m/s2,求:
如图所示,质量m=20kg的物体以水平速度v0=5m/s滑到静止在光滑水平地面的平板小车上.小车质量M=80kg,物体在小车上滑行一段距离后相对于小车静止.已知物体与平板间的动摩擦因数μ=0.8,g取10m/s2,求: 如图所示,以水平转盘上有一个质量为m的物体离转轴的距离为r,转轴与物体间用一根细绳相连,物体和转盘间的最大静摩擦力等于重力的μ倍,细线所能承受的最大拉力为3?mg.
如图所示,以水平转盘上有一个质量为m的物体离转轴的距离为r,转轴与物体间用一根细绳相连,物体和转盘间的最大静摩擦力等于重力的μ倍,细线所能承受的最大拉力为3?mg.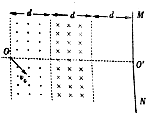 宽度都为d的两个区域存在磁感应强度大小相等的匀强磁场,但磁场方向相反,如图所示.足够大的屏MN与磁场最右侧边界的距离也等于d,直线OO′与磁场边界以及屏MN都垂直.质量为m、电荷量为e的电子从O点以速度v0射入磁场,速度方向与直线OO′成45°角.
宽度都为d的两个区域存在磁感应强度大小相等的匀强磁场,但磁场方向相反,如图所示.足够大的屏MN与磁场最右侧边界的距离也等于d,直线OO′与磁场边界以及屏MN都垂直.质量为m、电荷量为e的电子从O点以速度v0射入磁场,速度方向与直线OO′成45°角.