题目内容
9.已知地球半径R约为6.4×106m,地球质量M约为6×1024kg,引力常量G为6.67×10-11Nm2/kg2,近地人造地球卫星的周期T近约为85min,估算月球到地心的距离.分析 月球绕地球运转时,由地球的万有引力提供向心力,根据万有引力定律和牛顿第二定律列式求解.
解答 解:对于月球,根据万有引力提供向心力,得 G$\frac{{M}_{地}{m}_{月}}{{r}^{2}}$=m$\frac{4{π}^{2}}{{T}^{2}}$r,T=27×24×3600s
对于近地卫星,有:G$\frac{{M}_{地}m}{{R}^{2}}$=m$\frac{4{π}^{2}}{{T}_{卫}^{2}}$R,T卫=85×60s
联立解得 r≈3.8×108m
答:月球到地心的距离约为3.8×108m.
点评 本题关键要建立构型,明确月球向心力的来源,根据万有引力定律和牛顿第二定律求解.

练习册系列答案
相关题目
19. (1)如图所示,螺旋测微器所示的读数是4.010mm.
(1)如图所示,螺旋测微器所示的读数是4.010mm.
(2)在用电流表和电压表测干电池的电动势和内电阻的实验中,一位同学根据实验测得的5组数据如表,请在方格纸上(见答卷)标出对应的坐标点(符号为“•”),画出U-I图线.利用图线可求出电源电动势E=1.45V,内电阻r=0.69Ω.
 (1)如图所示,螺旋测微器所示的读数是4.010mm.
(1)如图所示,螺旋测微器所示的读数是4.010mm.(2)在用电流表和电压表测干电池的电动势和内电阻的实验中,一位同学根据实验测得的5组数据如表,请在方格纸上(见答卷)标出对应的坐标点(符号为“•”),画出U-I图线.利用图线可求出电源电动势E=1.45V,内电阻r=0.69Ω.
| 1 | 2 | 3 | 4 | 5 | |
| I/A | 0.45 | 0.36 | 0.25 | 0.15 | 0.10 |
| U/V | 1.04 | 1.13 | 1.24 | 1.34 | 1.40 |
4.一个粗糙的水平转台以角速度ω匀速转动,转台上有一小物体恰能随转台同步做匀速圆周运动,则下列说法中正确的是( )
| A. | 若增大ω,物体将沿切线方向飞出 | |
| B. | 若增大ω,物体将沿曲线逐渐远离圆心 | |
| C. | 若减小ω,物体将沿曲线逐渐靠近圆心 | |
| D. | 若减小ω,物体仍做匀速圆周运动 |
1.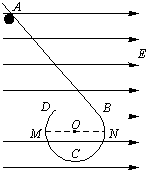 如图在光滑、绝缘的水平桌面上固定放置一光滑、绝缘的挡板ABCD,AB段为直线挡板,BCD段是半径为R的圆弧挡板,它们在B点平滑连接.挡板处于场强为E的水平向右的匀强电场中,电场方向与圆直径MN平行.现有一带电量为+q、质量为m的小球由静止从挡板内侧上的A点释放,并且小球能沿挡板内侧运动到D点抛出,则( )
如图在光滑、绝缘的水平桌面上固定放置一光滑、绝缘的挡板ABCD,AB段为直线挡板,BCD段是半径为R的圆弧挡板,它们在B点平滑连接.挡板处于场强为E的水平向右的匀强电场中,电场方向与圆直径MN平行.现有一带电量为+q、质量为m的小球由静止从挡板内侧上的A点释放,并且小球能沿挡板内侧运动到D点抛出,则( )
 如图在光滑、绝缘的水平桌面上固定放置一光滑、绝缘的挡板ABCD,AB段为直线挡板,BCD段是半径为R的圆弧挡板,它们在B点平滑连接.挡板处于场强为E的水平向右的匀强电场中,电场方向与圆直径MN平行.现有一带电量为+q、质量为m的小球由静止从挡板内侧上的A点释放,并且小球能沿挡板内侧运动到D点抛出,则( )
如图在光滑、绝缘的水平桌面上固定放置一光滑、绝缘的挡板ABCD,AB段为直线挡板,BCD段是半径为R的圆弧挡板,它们在B点平滑连接.挡板处于场强为E的水平向右的匀强电场中,电场方向与圆直径MN平行.现有一带电量为+q、质量为m的小球由静止从挡板内侧上的A点释放,并且小球能沿挡板内侧运动到D点抛出,则( )| A. | 小球从A点运动到N点的过程中,小球的速度一直在增大 | |
| B. | 小球在D点时的动能一定等于小球在B点时的动能 | |
| C. | 小球运动到C点时,挡板对小球的弹力一定大于mg | |
| D. | M点的位置一定在A点的右方 |
 细杆的一端与小球相连,可绕O点的水平轴自由转动,不计摩擦,杆长为R.
细杆的一端与小球相连,可绕O点的水平轴自由转动,不计摩擦,杆长为R.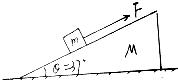 如图所示,有一斜劈质量为M=4kg,倾角为θ=37°,斜劈静止,一质量m=2kg的木块在F=16N的水平拉力下,沿斜面匀速上滑,求地面对斜劈的支持力和摩擦力.
如图所示,有一斜劈质量为M=4kg,倾角为θ=37°,斜劈静止,一质量m=2kg的木块在F=16N的水平拉力下,沿斜面匀速上滑,求地面对斜劈的支持力和摩擦力. 如图所示,一根粗细和质量分布均匀的细绳两端分别固定在水平天花板上的PQ两点,绳子过P、Q点的切线与竖直方向均成α角,已知绳子的质量为m,求:
如图所示,一根粗细和质量分布均匀的细绳两端分别固定在水平天花板上的PQ两点,绳子过P、Q点的切线与竖直方向均成α角,已知绳子的质量为m,求: 如图所示,质量均为m的带电物体A和B静止地放在绝缘水平面上,它们与水平面间的动摩擦因数均为μ,物体A和B所带电荷量分别为+Q和+2Q,他们间的距离为r(A,B均为可视为质点),
如图所示,质量均为m的带电物体A和B静止地放在绝缘水平面上,它们与水平面间的动摩擦因数均为μ,物体A和B所带电荷量分别为+Q和+2Q,他们间的距离为r(A,B均为可视为质点), 如图所示,倾角θ=37°的斜面固定在水平面上.质量m=1.0kg的小物块受到沿斜面向上的F=9.0N的拉力作用,小物块由静止沿斜面向上运动.小物块与斜面间的动摩擦因数μ=0.25,在小物块沿斜面向上运动2m时,将拉力F撤去,(斜面足够长,取g=l0m/s2.sin37°=0.60,cos37°=0.80)
如图所示,倾角θ=37°的斜面固定在水平面上.质量m=1.0kg的小物块受到沿斜面向上的F=9.0N的拉力作用,小物块由静止沿斜面向上运动.小物块与斜面间的动摩擦因数μ=0.25,在小物块沿斜面向上运动2m时,将拉力F撤去,(斜面足够长,取g=l0m/s2.sin37°=0.60,cos37°=0.80)