��Ŀ����
5�� ��ͼ��ʾ����ˮƽת������һ������Ϊm��������ת��ľ���Ϊr��ת�����������һ��ϸ�������������ת�̼�����Ħ�������������Ħ̱���ϸ�����ܳ��ܵ��������Ϊ3?mg��
��ͼ��ʾ����ˮƽת������һ������Ϊm��������ת��ľ���Ϊr��ת�����������һ��ϸ�������������ת�̼�����Ħ�������������Ħ̱���ϸ�����ܳ��ܵ��������Ϊ3?mg����1�������ٶ�Ϊ��1=$\sqrt{\frac{��g}{2r}}$ʱ����ϸ��������T1��
��2�������ٶȦ�2=$\sqrt{\frac{3��g}{2r}}$ʱ����ϸ��������T2��
��3����ת��ת���������ٶȦ�m��
���� ��1����2�����������������Ħ����ʱ���Ż��������ӣ������ֻ�ɾ�Ħ�����ṩ������ʱ���ٽ���ٶȣ��ж������Ƿ���������
��3�����ӵ�������������Ħ�����ĺ����ṩ������������ţ�ٵڶ�������ʽ��������ٶȣ�
��� �⣺��1��������ֻ�ɾ�Ħ�����ṩ������ʱ������������Ϊ��mg����ʱ
��mg��m��2r
��ã��ء�$\sqrt{\frac{��g}{r}}$
�����ٶ�${��}_{1}=\sqrt{\frac{��g}{2r}}$ʱ�����ڦ�1��$\sqrt{\frac{��g}{r}}$������ϸ������T1=0��
��2�������ٶȦ�2=$\sqrt{\frac{3��g}{2r}}$ʱ��${T}_{2}+��mg=m{��}_{2}^{2}r$
���ԣ�${T}_{2}=m{��}_{2}^{2}r-��mg=m•\frac{3��g}{2r}•r-��mg=0.5��mg$
��3���������ﵽ���ʱ��ת���������ٶȦ�max
${T}_{3}+��mg=m{��}_{m}^{2}r$
����3��mg+��mg=m${��}_{m}^{2}r$
����m=$\sqrt{\frac{4��g}{r}}=2\sqrt{\frac{��g}{r}}$
�𣺣�1�������ٶ�Ϊ��1=$\sqrt{\frac{��g}{2r}}$ʱ��ϸ����������0��
��2�������ٶȦ�2=$\sqrt{\frac{3��g}{2r}}$ʱ��ϸ����������0.5��mg��
��3��ת��ת���������ٶ���$2\sqrt{\frac{��g}{r}}$��
���� ����ؼ����ҵ���������Դ��ע����Ħ���������ṩ������ʱ�����Ӳű�����������С�α䣬����������

 ��ͼ��ʾ�����δ����ɾ�ֹ��ʼ���䴩���պ���Ȧ����Ȧ�в���������������һ��������˵������ȷ���ǣ�������
��ͼ��ʾ�����δ����ɾ�ֹ��ʼ���䴩���պ���Ȧ����Ȧ�в���������������һ��������˵������ȷ���ǣ�������| A�� | ���δ������������ܺͶ���֮���ڼ��� | |
| B�� | ��Ȧ�����δ��������������������� | |
| C�� | ������Ȧ�Ĵ�ͨ��һֱ���� | |
| D�� | ���δ����൱��һ����Դ |

| A�� | t1ʱ����������ʼ�����½� | |
| B�� | t2-t3ʱ�������������ھ�ֹ״̬ | |
| C�� | t3-t4���������ڳ���״̬ | |
| D�� | ��������t1��ʼ�������ϼ��١����١����٣����ͣ�ڽϸߵ�¥�㴦 |
 ������ȫ��ͬ�����1��2��3����ˮƽ�����ϣ������������Ķ�Ħ����������ͬ�����ô�С��ͬ������F��ͼʾ����ֱ�������1��2�ϣ���F��������ˮƽ����������3�ϣ�ʹ���߶��������˶�����a1��a2��a3�ֱ�������1��2��3�ļ��ٶȣ�������
������ȫ��ͬ�����1��2��3����ˮƽ�����ϣ������������Ķ�Ħ����������ͬ�����ô�С��ͬ������F��ͼʾ����ֱ�������1��2�ϣ���F��������ˮƽ����������3�ϣ�ʹ���߶��������˶�����a1��a2��a3�ֱ�������1��2��3�ļ��ٶȣ�������| A�� | a1=a2=a3 | B�� | a1=a2��a2��a3 | C�� | a1��a2��a2��a3 | D�� | a1��a2��a2��a3 |
 ϸ�˵�һ����С������������O���ˮƽ������ת��������Ħ�����˳�ΪR��
ϸ�˵�һ����С������������O���ˮƽ������ת��������Ħ�����˳�ΪR�� ��ͼ����Ǧ�=37���б����ֹ�ڵ��棬б������ΪM����б�����и�����Ϊm�����壬������б�������»�����֪��M=5kg��m=1kg����
��ͼ����Ǧ�=37���б����ֹ�ڵ��棬б������ΪM����б�����и�����Ϊm�����壬������б�������»�����֪��M=5kg��m=1kg����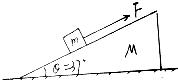 ��ͼ��ʾ����һб������ΪM=4kg�����Ϊ��=37�㣬б����ֹ��һ����m=2kg��ľ����F=16N��ˮƽ�����£���б�������ϻ���������б����֧������Ħ������
��ͼ��ʾ����һб������ΪM=4kg�����Ϊ��=37�㣬б����ֹ��һ����m=2kg��ľ����F=16N��ˮƽ�����£���б�������ϻ���������б����֧������Ħ������ ��ͼ��ʾ��һ����ϸ�������ֲ����ȵ�ϸ�����˷ֱ�̶���ˮƽ�컨���ϵ�PQ���㣬���ӹ�P��Q�����������ֱ������ɦ��ǣ���֪���ӵ�����Ϊm����
��ͼ��ʾ��һ����ϸ�������ֲ����ȵ�ϸ�����˷ֱ�̶���ˮƽ�컨���ϵ�PQ���㣬���ӹ�P��Q�����������ֱ������ɦ��ǣ���֪���ӵ�����Ϊm���� ��ͼ��ʾ��������ΧԲ���������з���ֱֽ���������ǿ�ų����Ÿ�Ӧǿ��ΪB��һ��������Բ�������ֱ���������ٶ�v����ų��������������ų��������˶��ķ�����ԭ���䷽��ɦȽǣ����������Ϊm�������Ϊe�����Ƶ���֮���������������ܵ���������
��ͼ��ʾ��������ΧԲ���������з���ֱֽ���������ǿ�ų����Ÿ�Ӧǿ��ΪB��һ��������Բ�������ֱ���������ٶ�v����ų��������������ų��������˶��ķ�����ԭ���䷽��ɦȽǣ����������Ϊm�������Ϊe�����Ƶ���֮���������������ܵ���������