题目内容
8. 两根足够长的固定的平行金属导轨位于同一水平面内,两导轨间的距离为L.导轨上面横放着两根导体棒a和b,构成矩形闭合回路,如图所示.两根导体棒的质量皆为m,电阻皆为R,回路中其余部分的电阻可不计.在整个导轨平面内都有竖直向上的匀强磁场.设两导体棒均可沿导轨无摩擦地滑行.t=0时,棒b静止,棒a受到水平向右的恒力F作用,经过时间t=t0棒a开始匀加速运动,则下列说法正确的是( )
两根足够长的固定的平行金属导轨位于同一水平面内,两导轨间的距离为L.导轨上面横放着两根导体棒a和b,构成矩形闭合回路,如图所示.两根导体棒的质量皆为m,电阻皆为R,回路中其余部分的电阻可不计.在整个导轨平面内都有竖直向上的匀强磁场.设两导体棒均可沿导轨无摩擦地滑行.t=0时,棒b静止,棒a受到水平向右的恒力F作用,经过时间t=t0棒a开始匀加速运动,则下列说法正确的是( )| A. | 当t>t0 时,b棒做匀速运动 | B. | 当t<t0 时,b棒做匀加速运动 | ||
| C. | 当t=2t0时,a棒加速度为$\frac{F}{m}$ | D. | 当t=2t0时,a棒加速度为$\frac{F}{2m}$ |
分析 分析t=t0时间内两导体棒的受力情况,再根据牛顿第二定律分析加速度的变化情况,由此得解.
解答 解:由于棒a受到水平向右的恒力F作用,开始一段时间内,随着a棒的速度增加,导体棒a受到的安培力增加,则a棒的加速度aa=$\frac{F-BIL}{m}$减小;对于b棒,随着安培力的增加,其加速度ab=$\frac{BIL}{m}$增加,当a和b的加速度达到相同时,二者的速度之差保持恒定,根据法拉第电磁感应定律和闭合电路的欧姆定律可得电流强度I=$\frac{BL△v}{R}$恒定,二者均做加速度相同的匀加速直线运动,由此可知:
A、当t>t0 时,b棒做匀加速运动,故A错误;
B、当t<t0 时,b棒做加速度增加的加速运动,故B错误;
CD、以整体为研究对象,当t=2t0时,根据牛顿第二定律可得a棒加速度为a=$\frac{F}{2m}$,故C错误、D正确.
故选:D.
点评 本题主要是考查了安培力作用下导体棒的运动问题,解答本题的关键是分析清楚两个导体棒的受力情况和运动情况.

练习册系列答案
相关题目
13. 如图所示,矩形虚线框MNPQ内有一匀强磁场,磁场方向垂直纸面向里,a、b、c是三个质量和电荷量都相等的带电粒子,它们从PQ边上的中点沿垂直于磁场的方向射入磁场,图中画出了它们在磁场中的运动轨迹,粒子重力不计.下列说法正确的是( )
如图所示,矩形虚线框MNPQ内有一匀强磁场,磁场方向垂直纸面向里,a、b、c是三个质量和电荷量都相等的带电粒子,它们从PQ边上的中点沿垂直于磁场的方向射入磁场,图中画出了它们在磁场中的运动轨迹,粒子重力不计.下列说法正确的是( )
 如图所示,矩形虚线框MNPQ内有一匀强磁场,磁场方向垂直纸面向里,a、b、c是三个质量和电荷量都相等的带电粒子,它们从PQ边上的中点沿垂直于磁场的方向射入磁场,图中画出了它们在磁场中的运动轨迹,粒子重力不计.下列说法正确的是( )
如图所示,矩形虚线框MNPQ内有一匀强磁场,磁场方向垂直纸面向里,a、b、c是三个质量和电荷量都相等的带电粒子,它们从PQ边上的中点沿垂直于磁场的方向射入磁场,图中画出了它们在磁场中的运动轨迹,粒子重力不计.下列说法正确的是( )| A. | 粒子a带负电 | |
| B. | 粒子C的动能最大 | |
| C. | 粒子b在磁场中运动的时间最长 | |
| D. | 粒子b在磁场中运动时间的向心力最大 |
17.下列现象中属于反冲运动的是( )
| A. | 喷气式飞机的运动 | B. | 直升机的运动 | ||
| C. | 火箭的运动 | D. | 用桨划船 |
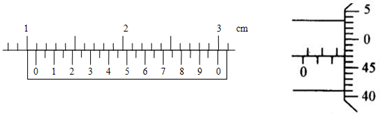 (1)图中游标卡尺的读数为10.90mm,螺旋测微器的读数为2.970mm.
(1)图中游标卡尺的读数为10.90mm,螺旋测微器的读数为2.970mm.
 如图所示,水平U形光滑框架,宽度为d=1m,MN间的电阻R=1.5Ω,导轨其它处电阻均不计,导体棒ab的质量m=0.2kg、电阻r=0.5Ω,匀强磁场的磁感应强度B=0.2T,方向垂直框架向下.现用F=1N的外力由静止开始向右拉ab棒,当ab棒的速度达到v=2m/s时,求:
如图所示,水平U形光滑框架,宽度为d=1m,MN间的电阻R=1.5Ω,导轨其它处电阻均不计,导体棒ab的质量m=0.2kg、电阻r=0.5Ω,匀强磁场的磁感应强度B=0.2T,方向垂直框架向下.现用F=1N的外力由静止开始向右拉ab棒,当ab棒的速度达到v=2m/s时,求: 如图所示,在光滑水平桌面上有一个闭合直角三角形导线框,在导线框右侧有一宽度为d的条形匀强磁场区域,d大于AC的边长,磁场的左边界与导线框BC边平行,磁场方向竖直向下,导线框以速度v向右匀速穿过匀强磁场区域.从BC边进入磁场区开始计时,到A点离开磁场区域为止的过程中,线框内感应电流随时间变化的情况(以逆时针方向为电流的正方向)是如图中所示的( )
如图所示,在光滑水平桌面上有一个闭合直角三角形导线框,在导线框右侧有一宽度为d的条形匀强磁场区域,d大于AC的边长,磁场的左边界与导线框BC边平行,磁场方向竖直向下,导线框以速度v向右匀速穿过匀强磁场区域.从BC边进入磁场区开始计时,到A点离开磁场区域为止的过程中,线框内感应电流随时间变化的情况(以逆时针方向为电流的正方向)是如图中所示的( )



 如图所示,电阻不计的平行金属导轨MN和OP水平放置,MO间接有阻值为R=0.5Ω的电阻,导轨相距为l=0.20m,其间有竖直向下的匀强磁场,磁感强度为B=0.50T,质量为m=0.1kg,电阻为r=0.5Ω的导体棒CD垂直于导轨放置,并接触良好.用平行于MN的恒力F=0.6N向右拉动CD.CD受恒定的摩擦阻力f=0.5N.求:
如图所示,电阻不计的平行金属导轨MN和OP水平放置,MO间接有阻值为R=0.5Ω的电阻,导轨相距为l=0.20m,其间有竖直向下的匀强磁场,磁感强度为B=0.50T,质量为m=0.1kg,电阻为r=0.5Ω的导体棒CD垂直于导轨放置,并接触良好.用平行于MN的恒力F=0.6N向右拉动CD.CD受恒定的摩擦阻力f=0.5N.求: