题目内容
7.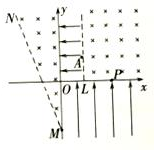 如图所示,在xoy坐标系的第一象限,y轴和x=L的虚线之间有一方向沿x轴负方向的匀强电场,电场强度大小为E0,第一象限虚线x=L的右侧有垂直纸面向里的匀强磁场.在y轴左侧及虚线MN之间也有垂直纸面向里的匀强磁场,M点的坐标为(0,-2L),MN与y轴正向的夹角为30°.在第四象限有沿y轴正向的匀强电场.一质量为m、带电量为q的带正电的粒子从电场中紧靠虚线x=L的A点由静止释放,A点的纵坐标y=L,结果粒子恰好不从MN穿出,粒子经第四象限的电场偏转后经x轴上的P点(2L,0)进入第一象限的磁场中,结果粒子从x=L的虚线上的D点垂直虚线进入第一象限的电场.不计粒子的重力,求:
如图所示,在xoy坐标系的第一象限,y轴和x=L的虚线之间有一方向沿x轴负方向的匀强电场,电场强度大小为E0,第一象限虚线x=L的右侧有垂直纸面向里的匀强磁场.在y轴左侧及虚线MN之间也有垂直纸面向里的匀强磁场,M点的坐标为(0,-2L),MN与y轴正向的夹角为30°.在第四象限有沿y轴正向的匀强电场.一质量为m、带电量为q的带正电的粒子从电场中紧靠虚线x=L的A点由静止释放,A点的纵坐标y=L,结果粒子恰好不从MN穿出,粒子经第四象限的电场偏转后经x轴上的P点(2L,0)进入第一象限的磁场中,结果粒子从x=L的虚线上的D点垂直虚线进入第一象限的电场.不计粒子的重力,求:(1)y轴左侧匀强磁场的磁感强强度的大小;
(2)第四象限内匀强电场的电场强度的大小;
(3)D点的坐标;
(4)粒子由A点运动到D点所用的时间.
分析 (1)根据动能定理,结合几何关系,与牛顿第二定律,即可求解磁感强强度的大小;
(2)依据运动的合成与分解,结合平抛运动处理的规律,即可求解电场强度的大小;
(3)根据粒子在磁场中做匀速圆周运动,结合几何关系,即可确定求解;
(4)做平抛运动时,依据运动学公式,求解运动时间;做圆周运动时,依据周期公式,求解运动轨迹对应的圆心角,即可求解时间.
解答 解:(1)粒子在第一象限的电场加速,依据动能定理,则有,qE0L=$\frac{1}{2}m{v}^{2}$;
粒子在y轴左侧磁场中做圆周运动,作出粒子在磁场中做圆周运动的轨迹,
MN与y轴正向的夹角为30°,
根据几何关系,有R+2R=3L
解得:R=L
根据牛顿第二定律,则有,qvB=m$\frac{{v}^{2}}{R}$
解得:B=$\frac{m\sqrt{\frac{2q{E}_{0}L}{m}}}{qL}$=$\sqrt{\frac{2{E}_{0}m}{qL}}$
(2)粒子进入第四象限内,在电场中做平抛运动,
根据运动的合成与分解,结合运动学公式,
则有,L=$\frac{1}{2}•\frac{qE}{m}{t}^{2}$
2L=vt
解得:E=E0;
(3)粒子从x轴上进入第一象限与x轴正向的夹角为θ=45°,由几何关系,在第一象限磁场中做圆周运动半径R′=$\sqrt{2}L$;
因此D点y坐标,y=L+$\sqrt{2}$L=(1+$\sqrt{2}$)L,即D点的坐标为(L,(1+$\sqrt{2}$)L);
(4)因L=$\frac{1}{2}•\frac{q{E}_{0}}{m}{t}_{1}^{2}$,那么在第一象限中运动时间t1=$\sqrt{\frac{2mL}{q{E}_{0}}}$;
在y轴左侧磁场中运动时间t2=$\frac{T}{2}$=$\frac{π}{2}\sqrt{\frac{2mL}{q{E}_{0}}}$
在第四象限电场中运动时间t3=$\frac{2L}{v}$=$\sqrt{\frac{2mL}{q{E}_{0}}}$;
在第一象限磁场中运动时间,t4=$\frac{2π×\sqrt{2}L×\frac{3}{8}}{\sqrt{2}v}$=$\frac{3π}{8}\sqrt{\frac{2mL}{q{E}_{0}}}$
则有,粒子由A点运动到D点所用的时间t4=t1+t2+t3+t4=(2$+\frac{7}{8}π$)$\sqrt{\frac{2mL}{q{E}_{0}}}$
答:(1)y轴左侧匀强磁场的磁感强强度的大小$\sqrt{\frac{2{E}_{0}m}{qL}}$;
(2)第四象限内匀强电场的电场强度的大小E0;
(3)D点的坐标(L,(1+$\sqrt{2}$)L);
(4)粒子由A点运动到D点所用的时间(2$+\frac{7}{8}π$)$\sqrt{\frac{2mL}{q{E}_{0}}}$.
点评 本题主要考查了带电粒子在混合场中运动的问题,要求同学们能正确分析粒子的受力情况,再通过受力情况分析粒子的运动情况,画出运动轨迹图,根据几何知识及圆周运动基本公式解答,同时掌握平抛运动规律,及运动的合成与分解内容,难度适中.

 一线名师权威作业本系列答案
一线名师权威作业本系列答案 某同学家中电视机画面的幅度偏小,维修的技术人员检查后认为是显像管或偏转线圈出了故障,显像管及偏转线圈l如图所示,引起故障的原因可能是( )
某同学家中电视机画面的幅度偏小,维修的技术人员检查后认为是显像管或偏转线圈出了故障,显像管及偏转线圈l如图所示,引起故障的原因可能是( )| A. | 电子枪发射的电子数减小 | |
| B. | 加速电场的电压过大 | |
| C. | 偏转线圈的电流过小,偏转磁场减弱 | |
| D. | 偏转线圈匝间短路,线圈匝数减小 |
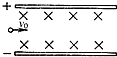 如图所示,一束重力不计带正电的粒子束,以速度v射入相互正交的匀强电场和匀速磁场组成的场区中.已知电场强度大小为E,方向竖直向下,磁场的磁感应强度大个为B,方向垂直于纸面向里.粒子束沿直线通过复合场区,则( )
如图所示,一束重力不计带正电的粒子束,以速度v射入相互正交的匀强电场和匀速磁场组成的场区中.已知电场强度大小为E,方向竖直向下,磁场的磁感应强度大个为B,方向垂直于纸面向里.粒子束沿直线通过复合场区,则( )| A. | 粒子的速度v=$\frac{B}{E}$ | |
| B. | 若粒子束变为负粒子,别粒子轨迹一定发生偏折 | |
| C. | 当v′>v时,粒子向下偏转 | |
| D. | 当v′<v时,粒子向下偏转 |
 如图所示,是将滑动变阻器作分压器用的电路,A、B为分压器的输出端,R是负载电阻,电源电压为U保持恒定,滑动片P位于变阻器的中央,下列判断正确的是( )
如图所示,是将滑动变阻器作分压器用的电路,A、B为分压器的输出端,R是负载电阻,电源电压为U保持恒定,滑动片P位于变阻器的中央,下列判断正确的是( )| A. | 空载(不接R)时,输出电压为$\frac{U}{2}$ | |
| B. | 接上负载R时,输出电压<$\frac{U}{2}$ | |
| C. | 负载电阻R的阻值越大,输出电压越低 | |
| D. | 接上负载R后,要使输出电压为$\frac{U}{2}$,滑片P须向下移动至某一位置 |
 在某静电场中,将一个带电量为q=+2.0×10-9C的质点由a移到b点,电场力做功为2.0×10-5J,再把该电荷由b点移到c点,克服电场力做功6.0×10-5J.
在某静电场中,将一个带电量为q=+2.0×10-9C的质点由a移到b点,电场力做功为2.0×10-5J,再把该电荷由b点移到c点,克服电场力做功6.0×10-5J.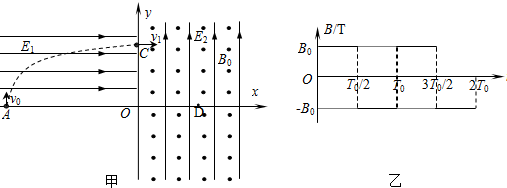 在竖直平面内建立一平面直角坐标系xoy,x轴沿水平方向,如图甲所示.第二象限内有一水平向右的匀强电场,场强为E1.坐标系的第一、四象限内有一正交的匀强电场和匀强交变磁场,电场方向竖直向上,场强E2=$\frac{1}{2}$E1,匀强磁场方向垂直纸面.处在第三象限的发射装置(图中未画出)竖直向上射出一个比荷$\frac{q}{m}$=102C/kg的带正电的粒子(可视为质点),该粒子以v0=4m/s的速度从-x上的A点进入第二象限,并以v1=8m/s速度从+y上的C点沿水平方向进入第一象限.取粒子刚进入第一象限的时刻为0时刻,磁感应强度按图乙所示规律变化(以垂直纸面向外的磁场方向为正方向),g=10m/s2.试求:
在竖直平面内建立一平面直角坐标系xoy,x轴沿水平方向,如图甲所示.第二象限内有一水平向右的匀强电场,场强为E1.坐标系的第一、四象限内有一正交的匀强电场和匀强交变磁场,电场方向竖直向上,场强E2=$\frac{1}{2}$E1,匀强磁场方向垂直纸面.处在第三象限的发射装置(图中未画出)竖直向上射出一个比荷$\frac{q}{m}$=102C/kg的带正电的粒子(可视为质点),该粒子以v0=4m/s的速度从-x上的A点进入第二象限,并以v1=8m/s速度从+y上的C点沿水平方向进入第一象限.取粒子刚进入第一象限的时刻为0时刻,磁感应强度按图乙所示规律变化(以垂直纸面向外的磁场方向为正方向),g=10m/s2.试求: 如图甲所示,MN、PQ为间距L=0.5m足够长的平行导轨,NQ⊥MN,导轨的电阻不计.导轨平面与水平面间的夹角θ=37°,NQ间连接有一个R=4Ω的电阻.有一匀强磁场垂直于导轨平面且方向向上,磁感应强度为B0=1T.将一根阻值未知质量为m=0.05kg的金属棒ab紧靠NQ放置在导轨上,且与导轨接触良好.现由静止释放金属棒,当金属棒滑行至cd处时达到稳定速度,已知在此过程中通过金属棒截面的电量q=0.2C,且金属棒的加速度a与速度v的关系如图乙所示,设金属棒沿导轨向下运动过程中始终与NQ平行.(取g=10m/s2,sin 37°=0.6,cos37°=0.8).求:
如图甲所示,MN、PQ为间距L=0.5m足够长的平行导轨,NQ⊥MN,导轨的电阻不计.导轨平面与水平面间的夹角θ=37°,NQ间连接有一个R=4Ω的电阻.有一匀强磁场垂直于导轨平面且方向向上,磁感应强度为B0=1T.将一根阻值未知质量为m=0.05kg的金属棒ab紧靠NQ放置在导轨上,且与导轨接触良好.现由静止释放金属棒,当金属棒滑行至cd处时达到稳定速度,已知在此过程中通过金属棒截面的电量q=0.2C,且金属棒的加速度a与速度v的关系如图乙所示,设金属棒沿导轨向下运动过程中始终与NQ平行.(取g=10m/s2,sin 37°=0.6,cos37°=0.8).求: 如图所示,真空室内有一个点状的α粒子放射源P,它向各个方向发射α粒子(不计重力),速率都相同,ab为P点附近的一条水平直线(P到直线ab的距离PC=L),Q为直线ab上一点,它与P点相距PQ=$\frac{\sqrt{5}}{2}$L(现只研究与放射源P和直线ab同一平面内的α粒子的运动),当真空室内(直线ab以上区域)只存在垂直该平面向里、磁感应强度为B的匀强磁场时,不同方向发射的α粒子若能到达ab直线,则到达ab直线时它们动能都相等,已知水平向左射出的α粒子也恰好到达Q点.(α粒子的电荷量为+q,质量为m,sin37°=0.6,cos37°=0.8)求:
如图所示,真空室内有一个点状的α粒子放射源P,它向各个方向发射α粒子(不计重力),速率都相同,ab为P点附近的一条水平直线(P到直线ab的距离PC=L),Q为直线ab上一点,它与P点相距PQ=$\frac{\sqrt{5}}{2}$L(现只研究与放射源P和直线ab同一平面内的α粒子的运动),当真空室内(直线ab以上区域)只存在垂直该平面向里、磁感应强度为B的匀强磁场时,不同方向发射的α粒子若能到达ab直线,则到达ab直线时它们动能都相等,已知水平向左射出的α粒子也恰好到达Q点.(α粒子的电荷量为+q,质量为m,sin37°=0.6,cos37°=0.8)求: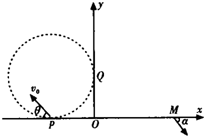 如图所示,在xOy平面的第Ⅱ象限内有半径为R的圆分别与x轴、y轴相切于P、Q两点,圆内存在垂直于xOy平面向外的匀强磁场.在第Ⅰ象限内存在沿y轴负方向的匀强电场,电场强度为E,一带正电的粒子(重力不计)以速度υ0从P点射入磁场后恰好垂直y轴进入电场,最后从M($\frac{8R}{3}$,0)点射出电场,出射方向与x轴正方向夹角为α,且满足tanα=$\frac{9}{8}$.
如图所示,在xOy平面的第Ⅱ象限内有半径为R的圆分别与x轴、y轴相切于P、Q两点,圆内存在垂直于xOy平面向外的匀强磁场.在第Ⅰ象限内存在沿y轴负方向的匀强电场,电场强度为E,一带正电的粒子(重力不计)以速度υ0从P点射入磁场后恰好垂直y轴进入电场,最后从M($\frac{8R}{3}$,0)点射出电场,出射方向与x轴正方向夹角为α,且满足tanα=$\frac{9}{8}$.