题目内容
19.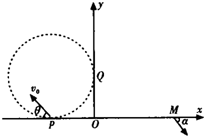 如图所示,在xOy平面的第Ⅱ象限内有半径为R的圆分别与x轴、y轴相切于P、Q两点,圆内存在垂直于xOy平面向外的匀强磁场.在第Ⅰ象限内存在沿y轴负方向的匀强电场,电场强度为E,一带正电的粒子(重力不计)以速度υ0从P点射入磁场后恰好垂直y轴进入电场,最后从M($\frac{8R}{3}$,0)点射出电场,出射方向与x轴正方向夹角为α,且满足tanα=$\frac{9}{8}$.
如图所示,在xOy平面的第Ⅱ象限内有半径为R的圆分别与x轴、y轴相切于P、Q两点,圆内存在垂直于xOy平面向外的匀强磁场.在第Ⅰ象限内存在沿y轴负方向的匀强电场,电场强度为E,一带正电的粒子(重力不计)以速度υ0从P点射入磁场后恰好垂直y轴进入电场,最后从M($\frac{8R}{3}$,0)点射出电场,出射方向与x轴正方向夹角为α,且满足tanα=$\frac{9}{8}$.求:(1)带电粒子的比荷;
(2)带电粒子在磁场中运动的时间.
分析 (1)粒子垂直于电场进入第一象限,粒子做类平抛运动,由到达M的速度方向可利用速度的合成与分解得知该点y方向的速度.结合牛顿第二定律求得粒子的比荷;
(2)根据运动学的公式,求出粒子进入电场时的位置,画出粒子运动的轨迹,根据图象中的几何关系求出粒子运动的半径;粒子在洛伦兹力的作用下做匀速圆周运动,利用洛伦兹力提供向心力的公式,求出在磁场中运动的轨迹半径,利用几何关系求偏转角θ,最后求出时间.
解答  解:(1)粒子垂直于电场进入第一象限,粒子做类平抛运动,设粒子沿y轴负方向做匀加速运动的加速度为a,
解:(1)粒子垂直于电场进入第一象限,粒子做类平抛运动,设粒子沿y轴负方向做匀加速运动的加速度为a,
qE=ma
设粒子在电场中运动的时间为t,在x轴方向上,粒子做匀速直线运动,有:$\frac{8R}{3}$=v0t ①
在M处,粒子沿y轴方向的分速度为:vy=v0tanα ②
vy=at ③
又据题意 tanα=$\frac{{v}_{y}}{{v}_{0}}$=$\frac{9}{8}$ ④
联立①②③④解得:$\frac{q}{m}=\frac{27{v}_{0}^{2}}{64ER}$
(2)又:y=$\frac{{v}_{y}}{2}•t$ ⑤
联立得:y=$\frac{3}{2}R$⑥
粒子的运动轨迹如图所示,O1是磁场圆的圆心,O2是粒子轨迹圆的圆心.P′是粒子射出磁场的位置,依题意知,粒子垂直y轴进入电场,则P′O∥PO1,且P′O1=PO1=R
所以粒子的轨道半径 r=R ⑦
由几何知识得:y=R+Rcos(180°-θ) ⑧
解得,θ=120°
粒子运动的周期:T=$\frac{2πr}{{v}_{0}}$=$\frac{2πR}{{v}_{0}}$
所以粒子运动的时间:t=$\frac{120°}{360°}•T=\frac{2πR}{3{v}_{0}}$
答:(l)带电粒子的比荷为$\frac{3{v}_{0}^{2}}{4ER}$;
(2)带电粒子在磁场中运动的时间是$\frac{2πR}{3{v}_{0}}$.
点评 粒子在电场中运动偏转时,常用能量的观点来解决问题,有时也要运用运动的合成与分解.粒子在磁场中做匀速圆周运动的圆心、半径及运动时间的确定也是本题的一个考查重点,要正确画出粒子运动的轨迹图,能熟练运用几何知识解决物理问题.

 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案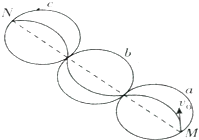 如图所示,a、b、c是面积相等的三个圆形匀强磁场区域,图中的虚线是三个圆直径的连线,该虚线与水平方向的夹角为45°.一不计重力的带电粒子,从a磁场的M点以初速度v0竖直向上射入磁场,运动轨迹如图,最后粒子从c磁场的N点离开磁场.已知粒子的质量为m,电荷量为q,匀强磁场的磁感应强度大小为B,则( )
如图所示,a、b、c是面积相等的三个圆形匀强磁场区域,图中的虚线是三个圆直径的连线,该虚线与水平方向的夹角为45°.一不计重力的带电粒子,从a磁场的M点以初速度v0竖直向上射入磁场,运动轨迹如图,最后粒子从c磁场的N点离开磁场.已知粒子的质量为m,电荷量为q,匀强磁场的磁感应强度大小为B,则( )| A. | a和c磁场的方向垂直于纸面向里,b磁场的方向垂直于纸面向外 | |
| B. | 粒子在N点的速度方向水平向右 | |
| C. | 粒子从M点运动到N点的时间为$\frac{3πm}{2qB}$ | |
| D. | 粒子从M点运动到N点的时间为$\frac{6πm}{qB}$ |
 北京正负电子对撞机重大改造工程曾获中国十大科技殊荣,储存环是北京正负电子对撞机中非常关键的组成部分,如图为储存环装置示意图.现将质子(${\;}_{1}^{1}$H)和α粒子(${\;}_{2}^{4}$He)等带电粒子储存在储存环空腔中,储存环置于一个与圆环平面垂直的匀强磁场(偏转磁场)中,磁感应强度为B.如果质子和α粒子在空腔中做圆周运动的轨迹相同(如图中虚线所示),偏转磁场也相同.比较质子和α粒子在圆环状空腔中运动的动能EH和Eα,运动的周期TH和Tα的大小,有( )
北京正负电子对撞机重大改造工程曾获中国十大科技殊荣,储存环是北京正负电子对撞机中非常关键的组成部分,如图为储存环装置示意图.现将质子(${\;}_{1}^{1}$H)和α粒子(${\;}_{2}^{4}$He)等带电粒子储存在储存环空腔中,储存环置于一个与圆环平面垂直的匀强磁场(偏转磁场)中,磁感应强度为B.如果质子和α粒子在空腔中做圆周运动的轨迹相同(如图中虚线所示),偏转磁场也相同.比较质子和α粒子在圆环状空腔中运动的动能EH和Eα,运动的周期TH和Tα的大小,有( )| A. | EH=Eα,TH≠Tα | B. | EH=Eα,TH=Tα | C. | EH≠Eα,TH≠Tα | D. | EH≠Eα,TH=Tα |
| A. | 电容是描述电容器容纳电荷本领大小的物理量 | |
| B. | 电容器是储存电荷和电能的容器,只有带电时才称电容器 | |
| C. | 固定电容器所充电荷量跟加在两极板间的电压成正比 | |
| D. | 电容器的电容跟极板所带电荷量成正比,跟极板间电压成反比 |
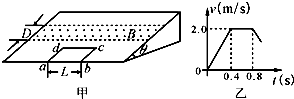 如图甲所示,表面绝缘、倾角θ=30°的足够长的斜面固定在水平地面上,斜面所在空间有一宽度D=0.40m的匀强磁场区域,其边界与斜面底边平行,磁场方向垂直斜面向上.一个质量m=0.10kg、总电阻R=0.25Ω的单匝矩形金属框abcd放在斜面的底端,其中ab边与斜面底边重合,ab边长L=0.50m.从t=0时刻开始,线框在垂直cd边沿斜面向上大小恒定的拉力作用下,从静止开始运动,当线框的ab边离开磁场区域时撤去拉力,让线框自由滑动,线框的速度与时间的关系如图乙所示.已知线框在整个运动过程中始终未脱离斜面,且保持ab边与斜面底边平行,线框与斜面之间的动摩擦因数μ=$\frac{\sqrt{3}}{3}$,重力加速度g取10m/s2.求:
如图甲所示,表面绝缘、倾角θ=30°的足够长的斜面固定在水平地面上,斜面所在空间有一宽度D=0.40m的匀强磁场区域,其边界与斜面底边平行,磁场方向垂直斜面向上.一个质量m=0.10kg、总电阻R=0.25Ω的单匝矩形金属框abcd放在斜面的底端,其中ab边与斜面底边重合,ab边长L=0.50m.从t=0时刻开始,线框在垂直cd边沿斜面向上大小恒定的拉力作用下,从静止开始运动,当线框的ab边离开磁场区域时撤去拉力,让线框自由滑动,线框的速度与时间的关系如图乙所示.已知线框在整个运动过程中始终未脱离斜面,且保持ab边与斜面底边平行,线框与斜面之间的动摩擦因数μ=$\frac{\sqrt{3}}{3}$,重力加速度g取10m/s2.求: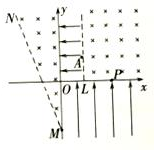 如图所示,在xoy坐标系的第一象限,y轴和x=L的虚线之间有一方向沿x轴负方向的匀强电场,电场强度大小为E0,第一象限虚线x=L的右侧有垂直纸面向里的匀强磁场.在y轴左侧及虚线MN之间也有垂直纸面向里的匀强磁场,M点的坐标为(0,-2L),MN与y轴正向的夹角为30°.在第四象限有沿y轴正向的匀强电场.一质量为m、带电量为q的带正电的粒子从电场中紧靠虚线x=L的A点由静止释放,A点的纵坐标y=L,结果粒子恰好不从MN穿出,粒子经第四象限的电场偏转后经x轴上的P点(2L,0)进入第一象限的磁场中,结果粒子从x=L的虚线上的D点垂直虚线进入第一象限的电场.不计粒子的重力,求:
如图所示,在xoy坐标系的第一象限,y轴和x=L的虚线之间有一方向沿x轴负方向的匀强电场,电场强度大小为E0,第一象限虚线x=L的右侧有垂直纸面向里的匀强磁场.在y轴左侧及虚线MN之间也有垂直纸面向里的匀强磁场,M点的坐标为(0,-2L),MN与y轴正向的夹角为30°.在第四象限有沿y轴正向的匀强电场.一质量为m、带电量为q的带正电的粒子从电场中紧靠虚线x=L的A点由静止释放,A点的纵坐标y=L,结果粒子恰好不从MN穿出,粒子经第四象限的电场偏转后经x轴上的P点(2L,0)进入第一象限的磁场中,结果粒子从x=L的虚线上的D点垂直虚线进入第一象限的电场.不计粒子的重力,求:
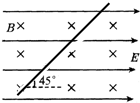 质量为m,带电量为q的微粒,以速度v与水平方向成45°角进入匀强电场和匀强磁场同时存在的空间(如图所示),微粒在电场、磁场、重力场的共同作用下做匀速直线运动,则带电粒子运动方向为沿轨迹向右上方,带电粒子带正电;电场强度大小为$\frac{mg}{q}$,磁感应强度的大小为$\frac{\sqrt{2}mg}{qv}$.
质量为m,带电量为q的微粒,以速度v与水平方向成45°角进入匀强电场和匀强磁场同时存在的空间(如图所示),微粒在电场、磁场、重力场的共同作用下做匀速直线运动,则带电粒子运动方向为沿轨迹向右上方,带电粒子带正电;电场强度大小为$\frac{mg}{q}$,磁感应强度的大小为$\frac{\sqrt{2}mg}{qv}$.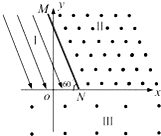 如图所示,平面直角坐标系xoy位于竖直平面内,M是一块与y轴夹角30°的挡板,与y轴的交点坐标为(0,$\sqrt{3}$L),下端无限接近x轴上的N点,粒子若打在挡板上会被挡板吸收.挡板左侧与x轴之间的区域Ⅰ内存在平行于挡板方向斜向下的匀强电场,电场强度大小为E.挡板右侧与x轴之间的区域Ⅱ内存在垂直纸面向外的匀强磁场,磁感应强度为2B,x轴下方区域Ⅲ存在垂直纸面向外的匀强磁场,磁感应强度大小为B.坐标原点o有两个质量均为m,电荷量分别为+q的粒子a和-q的粒子b,以及一个不带电的粒子c.空气阻力和粒子重力均不计,q>0. 求:
如图所示,平面直角坐标系xoy位于竖直平面内,M是一块与y轴夹角30°的挡板,与y轴的交点坐标为(0,$\sqrt{3}$L),下端无限接近x轴上的N点,粒子若打在挡板上会被挡板吸收.挡板左侧与x轴之间的区域Ⅰ内存在平行于挡板方向斜向下的匀强电场,电场强度大小为E.挡板右侧与x轴之间的区域Ⅱ内存在垂直纸面向外的匀强磁场,磁感应强度为2B,x轴下方区域Ⅲ存在垂直纸面向外的匀强磁场,磁感应强度大小为B.坐标原点o有两个质量均为m,电荷量分别为+q的粒子a和-q的粒子b,以及一个不带电的粒子c.空气阻力和粒子重力均不计,q>0. 求: