题目内容
3.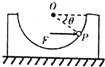 如图所示,质量为M的光滑半球形容器放在光滑水平面上,O为球心,一质量为m的小滑块(可视为质点)位于容器的P点,OP与水平方向成θ角,在水平恒力F的作用下,与容器保持相对静止做加速运动,下列关系正确的是( )
如图所示,质量为M的光滑半球形容器放在光滑水平面上,O为球心,一质量为m的小滑块(可视为质点)位于容器的P点,OP与水平方向成θ角,在水平恒力F的作用下,与容器保持相对静止做加速运动,下列关系正确的是( )| A. | 小滑块所受支持力FN=mgtanθ | B. | 小滑块所受支持力FN=$\frac{mg}{tanθ}$ | ||
| C. | 水平恒力F=$\frac{m(M+m)g}{Mtanθ}$ | D. | 水平恒力F=$\frac{mg}{tanθ}$ |
分析 对滑块受力分析,受重力、推力和支持力,运用正交分解法求出加速度a和支持力${F}_{N}^{\;}$,再对整体运用牛顿第二定律求水平恒力F;
解答 解:对滑块受力分析,如图所示:
竖直方向受力平衡条件,有:${F}_{N}^{\;}sinθ=mg$,得${F}_{N}^{\;}=\frac{mg}{sinθ}$
水平方向:$F-{F}_{N}^{\;}cosθ=ma$,得$a=\frac{F}{m}-\frac{g}{tanθ}$,故AB错误;
对整体,根据牛顿第二定律:F=(M+m)a
解得:$F=\frac{m(M+m)g}{Mtanθ}$,故C正确,D错误;
故选:C
点评 本题考查牛顿定律的应用,关键是运用整体法和隔离法进行受力分析,作出力图是解题的关键,在力图上要标出相关角度,方便解答.

练习册系列答案
 高效智能课时作业系列答案
高效智能课时作业系列答案 捷径训练检测卷系列答案
捷径训练检测卷系列答案
相关题目
14.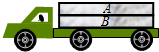 如图所示,钢铁构件A、B叠放在卡车的水平底板上,卡车底板和B间动摩擦因数为μ1,A、B间动摩擦因数为μ2,μ1>μ2,卡车刹车的最大加速度为a,a>μ1g,可以认为最大静摩擦力与滑动摩擦力大小相等.卡车沿平直公路行驶途中遇到紧急情况时,要求其刹车后在s0距离内能安全停下,则卡车行驶的速度不能超过( )
如图所示,钢铁构件A、B叠放在卡车的水平底板上,卡车底板和B间动摩擦因数为μ1,A、B间动摩擦因数为μ2,μ1>μ2,卡车刹车的最大加速度为a,a>μ1g,可以认为最大静摩擦力与滑动摩擦力大小相等.卡车沿平直公路行驶途中遇到紧急情况时,要求其刹车后在s0距离内能安全停下,则卡车行驶的速度不能超过( )
 如图所示,钢铁构件A、B叠放在卡车的水平底板上,卡车底板和B间动摩擦因数为μ1,A、B间动摩擦因数为μ2,μ1>μ2,卡车刹车的最大加速度为a,a>μ1g,可以认为最大静摩擦力与滑动摩擦力大小相等.卡车沿平直公路行驶途中遇到紧急情况时,要求其刹车后在s0距离内能安全停下,则卡车行驶的速度不能超过( )
如图所示,钢铁构件A、B叠放在卡车的水平底板上,卡车底板和B间动摩擦因数为μ1,A、B间动摩擦因数为μ2,μ1>μ2,卡车刹车的最大加速度为a,a>μ1g,可以认为最大静摩擦力与滑动摩擦力大小相等.卡车沿平直公路行驶途中遇到紧急情况时,要求其刹车后在s0距离内能安全停下,则卡车行驶的速度不能超过( )| A. | $\sqrt{2a{s}_{0}}$ | B. | $\sqrt{2{μ}_{1}g{s}_{0}}$ | C. | $\sqrt{2{μ}_{2}g{s}_{0}}$ | D. | $\sqrt{({μ}_{1}+{μ}_{2})g{s}_{0}}$ |
8. 一小滑块(可看成质点)在水平拉力F作用下,沿粗糙水平面上做直线运动,其速度v随时间t变化的图象如图所示.在0.5s、1.5s、2.5s、3.5s时刻拉力F的大小分别为F1、F2、F3、F4,则下列判断一定正确的是( )
一小滑块(可看成质点)在水平拉力F作用下,沿粗糙水平面上做直线运动,其速度v随时间t变化的图象如图所示.在0.5s、1.5s、2.5s、3.5s时刻拉力F的大小分别为F1、F2、F3、F4,则下列判断一定正确的是( )
 一小滑块(可看成质点)在水平拉力F作用下,沿粗糙水平面上做直线运动,其速度v随时间t变化的图象如图所示.在0.5s、1.5s、2.5s、3.5s时刻拉力F的大小分别为F1、F2、F3、F4,则下列判断一定正确的是( )
一小滑块(可看成质点)在水平拉力F作用下,沿粗糙水平面上做直线运动,其速度v随时间t变化的图象如图所示.在0.5s、1.5s、2.5s、3.5s时刻拉力F的大小分别为F1、F2、F3、F4,则下列判断一定正确的是( )| A. | F1<F2 | B. | F2=F3 | C. | F1>F4 | D. | F3>F4 |
12.质量M=1.5kg的手榴弹某时刻恰好沿水平方向运动,速度大小是20m/s,此时在空中爆炸,分裂成两部分,其中0.5kg的那部分以40m/s的速度与原速度反向运动,则另一部分此时速率为( )
| A. | 20 m/s | B. | 25 m/s | C. | 40 m/s | D. | 50 m/s |

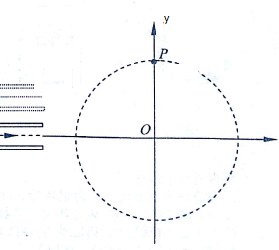 如图所示,在以坐标原点O为圆心半径为R的圆形区域内,存在磁感应强度大小为B的匀强磁场,磁场方向与纸面垂直.两块等大的金属板与x轴平行,金属板间有正交的匀强电场和磁场,其中磁场的磁感应强度大小为B0,一质量为m、电荷量为+q的粒子甲,在两板间沿与两板中线重合的x轴运动并进入圆形区域,结果粒子从y轴上的P(0,R)点离开磁场;若将两金属板同时沿y轴正方向移动$\frac{R}{2}$至图中虚线位置,让质量为m、电荷量为-q的粒子乙,以与甲相同的初速度沿两板中线射入两板间,经过一段时间粒子乙从y轴上的一点离开圆形区域.求:(不计粒子重力)
如图所示,在以坐标原点O为圆心半径为R的圆形区域内,存在磁感应强度大小为B的匀强磁场,磁场方向与纸面垂直.两块等大的金属板与x轴平行,金属板间有正交的匀强电场和磁场,其中磁场的磁感应强度大小为B0,一质量为m、电荷量为+q的粒子甲,在两板间沿与两板中线重合的x轴运动并进入圆形区域,结果粒子从y轴上的P(0,R)点离开磁场;若将两金属板同时沿y轴正方向移动$\frac{R}{2}$至图中虚线位置,让质量为m、电荷量为-q的粒子乙,以与甲相同的初速度沿两板中线射入两板间,经过一段时间粒子乙从y轴上的一点离开圆形区域.求:(不计粒子重力)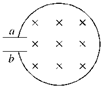 如图所示,线圈面积S=1×10-3m2,匝数n=100,两端点连接一电容器,其电容C=30 μF.线圈中磁场的磁感应强度按$\frac{△B}{△t}$=0.1T/s增加,磁场方向垂直线圈平面向里,那么电容器所带电荷量为$3×1{0}_{\;}^{-7}C$电容器的极板a带正电(填“正”或“负”).
如图所示,线圈面积S=1×10-3m2,匝数n=100,两端点连接一电容器,其电容C=30 μF.线圈中磁场的磁感应强度按$\frac{△B}{△t}$=0.1T/s增加,磁场方向垂直线圈平面向里,那么电容器所带电荷量为$3×1{0}_{\;}^{-7}C$电容器的极板a带正电(填“正”或“负”). 某同学想测出济南当地的重力加速度g,并验证机械能守恒定律.为了减小误差,他设计了一个实验如下:将一根长直铝棒用细线悬挂在空中(如图甲所示),在靠近铝棒下端的一侧固定电动机M,使电动机转轴处于竖直方向,在转轴上水平固定一支特制笔N,借助转动时的现象,将墨汁甩出形成一条细线.调整笔的位置,使墨汁在棒上能清晰地留下墨线.启动电动机待转速稳定后,用火烧断悬线,让铝棒自由下落,笔在铝棒上相应位置留下墨线.图乙是实验时在铝棒上所留下的墨线,将某条合适的墨线A作为起始线,此后每隔4条墨线取一条计数墨线,分别记作B、C、D、E.将最小刻度为毫米的刻度尺的零刻度线对准A,此时B、C、D、E对应的刻度依次为14.68cm、39.15cm、73.41cm、117.46cm.已知电动机的转速为3000r/min.求:
某同学想测出济南当地的重力加速度g,并验证机械能守恒定律.为了减小误差,他设计了一个实验如下:将一根长直铝棒用细线悬挂在空中(如图甲所示),在靠近铝棒下端的一侧固定电动机M,使电动机转轴处于竖直方向,在转轴上水平固定一支特制笔N,借助转动时的现象,将墨汁甩出形成一条细线.调整笔的位置,使墨汁在棒上能清晰地留下墨线.启动电动机待转速稳定后,用火烧断悬线,让铝棒自由下落,笔在铝棒上相应位置留下墨线.图乙是实验时在铝棒上所留下的墨线,将某条合适的墨线A作为起始线,此后每隔4条墨线取一条计数墨线,分别记作B、C、D、E.将最小刻度为毫米的刻度尺的零刻度线对准A,此时B、C、D、E对应的刻度依次为14.68cm、39.15cm、73.41cm、117.46cm.已知电动机的转速为3000r/min.求: 如图所示,在倾角为θ的光滑斜面上有两个用轻质弹簧相连接的物块A、B,它们的质量分别为mA、mB,弹簧的劲度系数为k,C为一固定挡板.系统处于静止状态.现开始用一恒力F沿斜面方向拉物块A使之向上运动.(重力加速度为g)求:
如图所示,在倾角为θ的光滑斜面上有两个用轻质弹簧相连接的物块A、B,它们的质量分别为mA、mB,弹簧的劲度系数为k,C为一固定挡板.系统处于静止状态.现开始用一恒力F沿斜面方向拉物块A使之向上运动.(重力加速度为g)求: