题目内容
6. 如图所示,在倾角为θ的光滑斜面上有两个用轻质弹簧相连接的物块A、B,它们的质量分别为mA、mB,弹簧的劲度系数为k,C为一固定挡板.系统处于静止状态.现开始用一恒力F沿斜面方向拉物块A使之向上运动.(重力加速度为g)求:
如图所示,在倾角为θ的光滑斜面上有两个用轻质弹簧相连接的物块A、B,它们的质量分别为mA、mB,弹簧的劲度系数为k,C为一固定挡板.系统处于静止状态.现开始用一恒力F沿斜面方向拉物块A使之向上运动.(重力加速度为g)求:(1)物块B刚要离开C时,物块A的位移x为多少?
(2)物块B刚要离开C时,物块A的加速度多大?
分析 (1)先对木块A受力分析,受重力,斜面的支持力和弹簧的弹力,根据共点力平衡条件求出弹簧的弹力后,再得到弹簧的压缩量;物块B刚要离开C时,先对物块B受力分析,受重力、支持力和弹簧的拉力,根据平衡条件求出弹簧弹力后进一步得到弹簧的伸长量,从而得到物体A的位移x;
(2)再对物体A受力分析,受到拉力F、重力、支持力和弹簧的弹力,根据牛顿第二定律求出加速度.
解答 解:(1)A不受力静止时,弹簧处于压缩状态,设此时弹簧压缩量为x1,
分析A物体受力可知:kx1=mAgsinθ,
得 x1=$\frac{{m}_{A}gsinθ}{k}$
在恒力作用下,A向上加速运动,弹簧由压缩状态逐渐变为伸长状态.当B刚要离开C时,弹簧的伸长量设为x2,分析B的受力有:
kx2=mBgsinθ,
得 x2=$\frac{{m}_{B}gsinθ}{k}$
物块A的位移 x=x1+x2=$\frac{({m}_{A}+{m}_{B})gsinθ}{k}$
(2)设此时A的加速度为a,由牛顿第二定律有:
F-mAgsinθ-kx2=mAa,
得 a=$\frac{F-({m}_{A}+{m}_{B})gsinθ}{{m}_{A}}$
答:
(1)物块B刚要离开C时,物块A的位移x为$\frac{({m}_{A}+{m}_{B})gsinθ}{k}$.
(2)物块B刚要离开C时,物块A的加速度为$\frac{F-({m}_{A}+{m}_{B})gsinθ}{{m}_{A}}$.
点评 本题关键要多次对物体A和B受力分析,求出弹簧的弹力,最后再根据牛顿第二定律求解加速度.

练习册系列答案
相关题目
3.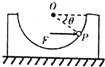 如图所示,质量为M的光滑半球形容器放在光滑水平面上,O为球心,一质量为m的小滑块(可视为质点)位于容器的P点,OP与水平方向成θ角,在水平恒力F的作用下,与容器保持相对静止做加速运动,下列关系正确的是( )
如图所示,质量为M的光滑半球形容器放在光滑水平面上,O为球心,一质量为m的小滑块(可视为质点)位于容器的P点,OP与水平方向成θ角,在水平恒力F的作用下,与容器保持相对静止做加速运动,下列关系正确的是( )
 如图所示,质量为M的光滑半球形容器放在光滑水平面上,O为球心,一质量为m的小滑块(可视为质点)位于容器的P点,OP与水平方向成θ角,在水平恒力F的作用下,与容器保持相对静止做加速运动,下列关系正确的是( )
如图所示,质量为M的光滑半球形容器放在光滑水平面上,O为球心,一质量为m的小滑块(可视为质点)位于容器的P点,OP与水平方向成θ角,在水平恒力F的作用下,与容器保持相对静止做加速运动,下列关系正确的是( )| A. | 小滑块所受支持力FN=mgtanθ | B. | 小滑块所受支持力FN=$\frac{mg}{tanθ}$ | ||
| C. | 水平恒力F=$\frac{m(M+m)g}{Mtanθ}$ | D. | 水平恒力F=$\frac{mg}{tanθ}$ |
4. 电路如图所示,a、b是两个完全相同的灯泡,L是一个直流电阻很小而自感系数很大的自感线圈.下列说法中正确的是( )
电路如图所示,a、b是两个完全相同的灯泡,L是一个直流电阻很小而自感系数很大的自感线圈.下列说法中正确的是( )
 电路如图所示,a、b是两个完全相同的灯泡,L是一个直流电阻很小而自感系数很大的自感线圈.下列说法中正确的是( )
电路如图所示,a、b是两个完全相同的灯泡,L是一个直流电阻很小而自感系数很大的自感线圈.下列说法中正确的是( )| A. | 闭合S时,a、b同时亮,而且亮度相同 | |
| B. | 闭合S时,b始终不亮,a逐渐亮起来后保持亮度不变 | |
| C. | 断开S时,a灯立即灭,b灯由暗变亮后逐渐熄灭 | |
| D. | 断开S时,a、b两灯都立即灭 |
11. 如图所示,在边长ab=1.5L,bc=$\sqrt{3}$L的矩形区域存在着垂直纸面向里、磁感应强度为B的匀强磁场,在ad边中心O点处有一粒子源,可以垂直磁场向区域内各方向发射速度大小相等的同种带电粒子.若沿Od方向射入的粒子从磁场边界cd离开磁场,该粒子在磁场中运动的时间为t0,圆周运动半径为L,不计粒子的重力和粒子间的相互作用.下列说法正确的是( )
如图所示,在边长ab=1.5L,bc=$\sqrt{3}$L的矩形区域存在着垂直纸面向里、磁感应强度为B的匀强磁场,在ad边中心O点处有一粒子源,可以垂直磁场向区域内各方向发射速度大小相等的同种带电粒子.若沿Od方向射入的粒子从磁场边界cd离开磁场,该粒子在磁场中运动的时间为t0,圆周运动半径为L,不计粒子的重力和粒子间的相互作用.下列说法正确的是( )
 如图所示,在边长ab=1.5L,bc=$\sqrt{3}$L的矩形区域存在着垂直纸面向里、磁感应强度为B的匀强磁场,在ad边中心O点处有一粒子源,可以垂直磁场向区域内各方向发射速度大小相等的同种带电粒子.若沿Od方向射入的粒子从磁场边界cd离开磁场,该粒子在磁场中运动的时间为t0,圆周运动半径为L,不计粒子的重力和粒子间的相互作用.下列说法正确的是( )
如图所示,在边长ab=1.5L,bc=$\sqrt{3}$L的矩形区域存在着垂直纸面向里、磁感应强度为B的匀强磁场,在ad边中心O点处有一粒子源,可以垂直磁场向区域内各方向发射速度大小相等的同种带电粒子.若沿Od方向射入的粒子从磁场边界cd离开磁场,该粒子在磁场中运动的时间为t0,圆周运动半径为L,不计粒子的重力和粒子间的相互作用.下列说法正确的是( )| A. | 粒子带负电 | |
| B. | 粒子在磁场中做匀速圆周运动的周期为4t0 | |
| C. | 粒子的比荷为$\frac{π}{B{t}_{0}}$ | |
| D. | 粒子在磁场中运动的最长时间为2t0 |
15.物体从静止开始以2m/s2的加速度作匀加速直线运动,则物体( )
| A. | 第1s内通过的位移是2m | B. | 第1s末的速度是2m/s | ||
| C. | 第1s内的平均速度是2m/s | D. | 第3s初的速度是6m/s |

 图示为沿x轴正方向传播的简谐波在t=0时的波形图,此时x=5m处的质点刚开始振动,一个人观察x=3m处的P点,发现在3s内P点经过的路程为60cm.求:
图示为沿x轴正方向传播的简谐波在t=0时的波形图,此时x=5m处的质点刚开始振动,一个人观察x=3m处的P点,发现在3s内P点经过的路程为60cm.求: