题目内容
14. 如图所示,钢铁构件A、B叠放在卡车的水平底板上,卡车底板和B间动摩擦因数为μ1,A、B间动摩擦因数为μ2,μ1>μ2,卡车刹车的最大加速度为a,a>μ1g,可以认为最大静摩擦力与滑动摩擦力大小相等.卡车沿平直公路行驶途中遇到紧急情况时,要求其刹车后在s0距离内能安全停下,则卡车行驶的速度不能超过( )
如图所示,钢铁构件A、B叠放在卡车的水平底板上,卡车底板和B间动摩擦因数为μ1,A、B间动摩擦因数为μ2,μ1>μ2,卡车刹车的最大加速度为a,a>μ1g,可以认为最大静摩擦力与滑动摩擦力大小相等.卡车沿平直公路行驶途中遇到紧急情况时,要求其刹车后在s0距离内能安全停下,则卡车行驶的速度不能超过( )| A. | $\sqrt{2a{s}_{0}}$ | B. | $\sqrt{2{μ}_{1}g{s}_{0}}$ | C. | $\sqrt{2{μ}_{2}g{s}_{0}}$ | D. | $\sqrt{({μ}_{1}+{μ}_{2})g{s}_{0}}$ |
分析 对物体受力分析,由牛顿第二定律求出加速度,然后求出最大加速度,再结合运动学的公式即可求出最大速度.
解答 解:设A、B的质量为m,以最大加速度运动时,A与B保持相对静止,A与B之间的摩擦力小于等于A与B之间的最大静摩擦力,由牛顿第二定律得:f1=ma1≤μ2mg,
解得:a1≤μ2g,
同理,可知B的最大加速度:a2≤μ1g
由于μ1>μ2,则a1<a2≤μ1g<a
可知要求其刹车后在s0距离内能安全停下,则车的最大加速度等于a1.
所以车的最大速度:vm=$\sqrt{2{μ}_{2}g{s}_{0}}$
故ABD错误,C正确
故选:C
点评 本题考查了求加速度、速度问题,分析清楚物体运动过程,应用牛顿第二定律、运动学公式 即可正确解题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
4. 如图,质量m=10kg的物块甲与质量为M=4kg长木板(足够长)乙一起在外力F的作用下向右做匀速运动,已知甲、乙之间动摩擦因数μ1=0.1,地面和长木板之间动摩擦因数μ2=0.2,则撤掉力F后(由于木板足够长,甲不会脱离木板),则下列说法错误的是( )
如图,质量m=10kg的物块甲与质量为M=4kg长木板(足够长)乙一起在外力F的作用下向右做匀速运动,已知甲、乙之间动摩擦因数μ1=0.1,地面和长木板之间动摩擦因数μ2=0.2,则撤掉力F后(由于木板足够长,甲不会脱离木板),则下列说法错误的是( )
 如图,质量m=10kg的物块甲与质量为M=4kg长木板(足够长)乙一起在外力F的作用下向右做匀速运动,已知甲、乙之间动摩擦因数μ1=0.1,地面和长木板之间动摩擦因数μ2=0.2,则撤掉力F后(由于木板足够长,甲不会脱离木板),则下列说法错误的是( )
如图,质量m=10kg的物块甲与质量为M=4kg长木板(足够长)乙一起在外力F的作用下向右做匀速运动,已知甲、乙之间动摩擦因数μ1=0.1,地面和长木板之间动摩擦因数μ2=0.2,则撤掉力F后(由于木板足够长,甲不会脱离木板),则下列说法错误的是( )| A. | 甲乙仍然相对静止,一起匀减速运动直至停止 | |
| B. | 在甲停止运动前,地面对乙的摩擦力大小始终不变 | |
| C. | 在甲停止运动前,乙的加速大小都是4.5m/s2 | |
| D. | 在乙停止运动前,甲的加速度大小始终为1m/s2 |
19. 如图所示,三角体由两种材料拼接而成,BC界面平行底面DE,两侧面与水平面夹角分别为30°和60°.已知物块从A静止下滑,加速至B匀速至D;若该物块静止从A沿另一侧面下滑,则有( )
如图所示,三角体由两种材料拼接而成,BC界面平行底面DE,两侧面与水平面夹角分别为30°和60°.已知物块从A静止下滑,加速至B匀速至D;若该物块静止从A沿另一侧面下滑,则有( )
 如图所示,三角体由两种材料拼接而成,BC界面平行底面DE,两侧面与水平面夹角分别为30°和60°.已知物块从A静止下滑,加速至B匀速至D;若该物块静止从A沿另一侧面下滑,则有( )
如图所示,三角体由两种材料拼接而成,BC界面平行底面DE,两侧面与水平面夹角分别为30°和60°.已知物块从A静止下滑,加速至B匀速至D;若该物块静止从A沿另一侧面下滑,则有( )| A. | 通过C点的速率可能等于通过B点的速率 | |
| B. | AB段的运动时间大于AC段的运动时间 | |
| C. | 物块将加速至C匀速至E | |
| D. | 一直加速运动到E,但AC段的加速度比CE段小 |
6.如图(甲)所示,平行光滑金属导轨水平放置,两轨相距L=0.4m,导轨一端与阻值R=0.3Ω的电阻相连,导轨电阻不计.导轨x>0一侧存在沿x方向均匀增大的恒定磁场,其方向与导轨平面垂直向下,磁感应强度B随位置x变化如图(乙)所示.一根质量m=0.2kg、电阻r=0.1Ω的金属棒置于导轨上,并与导轨垂直,棒在外力F作用下从x=0处以初速度v0=2m/s沿导轨向右变速运动,且金属棒在运动过程中受到的安培力大小不变.下列说法中正确的是( )
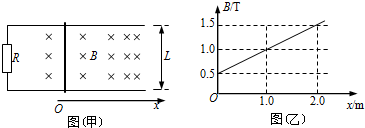
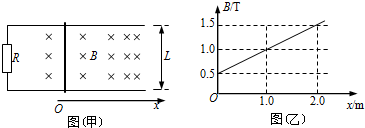
| A. | 金属棒向右做匀减速直线运动 | |
| B. | 金属棒在x=1 m处的速度大小为0.5m/s | |
| C. | 金属棒从x=0运动到x=1m过程中,外力F所做的功为-0.175 J | |
| D. | 金属棒从x=0运动到x=2m过程中,流过金属棒的电量为2C |
3.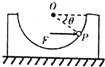 如图所示,质量为M的光滑半球形容器放在光滑水平面上,O为球心,一质量为m的小滑块(可视为质点)位于容器的P点,OP与水平方向成θ角,在水平恒力F的作用下,与容器保持相对静止做加速运动,下列关系正确的是( )
如图所示,质量为M的光滑半球形容器放在光滑水平面上,O为球心,一质量为m的小滑块(可视为质点)位于容器的P点,OP与水平方向成θ角,在水平恒力F的作用下,与容器保持相对静止做加速运动,下列关系正确的是( )
 如图所示,质量为M的光滑半球形容器放在光滑水平面上,O为球心,一质量为m的小滑块(可视为质点)位于容器的P点,OP与水平方向成θ角,在水平恒力F的作用下,与容器保持相对静止做加速运动,下列关系正确的是( )
如图所示,质量为M的光滑半球形容器放在光滑水平面上,O为球心,一质量为m的小滑块(可视为质点)位于容器的P点,OP与水平方向成θ角,在水平恒力F的作用下,与容器保持相对静止做加速运动,下列关系正确的是( )| A. | 小滑块所受支持力FN=mgtanθ | B. | 小滑块所受支持力FN=$\frac{mg}{tanθ}$ | ||
| C. | 水平恒力F=$\frac{m(M+m)g}{Mtanθ}$ | D. | 水平恒力F=$\frac{mg}{tanθ}$ |
4. 电路如图所示,a、b是两个完全相同的灯泡,L是一个直流电阻很小而自感系数很大的自感线圈.下列说法中正确的是( )
电路如图所示,a、b是两个完全相同的灯泡,L是一个直流电阻很小而自感系数很大的自感线圈.下列说法中正确的是( )
 电路如图所示,a、b是两个完全相同的灯泡,L是一个直流电阻很小而自感系数很大的自感线圈.下列说法中正确的是( )
电路如图所示,a、b是两个完全相同的灯泡,L是一个直流电阻很小而自感系数很大的自感线圈.下列说法中正确的是( )| A. | 闭合S时,a、b同时亮,而且亮度相同 | |
| B. | 闭合S时,b始终不亮,a逐渐亮起来后保持亮度不变 | |
| C. | 断开S时,a灯立即灭,b灯由暗变亮后逐渐熄灭 | |
| D. | 断开S时,a、b两灯都立即灭 |
 2016年新春佳节,我市的许多餐厅生意火爆,常常人满为患,为能服务更多的顾客,服务员需要用最短的时间将菜肴送至顾客处(设菜品送到顾客处速度恰好为零).某次服务员用单手托托盘方式(如图)给12m远处的顾客上菜,要求全程托盘水平.托盘和手、碗之间的摩擦因数分别为0.2、0.15,服务员上菜最大速度为3m/s.假设服务员加速、减速运动过程中是匀变速直线运动,且可认为最大静摩擦力等于滑动摩擦力.则:
2016年新春佳节,我市的许多餐厅生意火爆,常常人满为患,为能服务更多的顾客,服务员需要用最短的时间将菜肴送至顾客处(设菜品送到顾客处速度恰好为零).某次服务员用单手托托盘方式(如图)给12m远处的顾客上菜,要求全程托盘水平.托盘和手、碗之间的摩擦因数分别为0.2、0.15,服务员上菜最大速度为3m/s.假设服务员加速、减速运动过程中是匀变速直线运动,且可认为最大静摩擦力等于滑动摩擦力.则: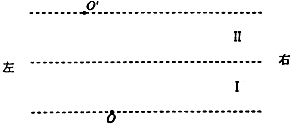 如图所示,真空中区域I和区域Ⅱ内存在着与纸面垂直的方向相反的匀强磁场,磁感应强度大小均为B.在区域II的上边界线上的N点固定一负的点电荷,并采取措施使之只对区域II以上空间产生影响.一带正电的粒子质量为m,电荷量为q,自区域I下边界线上的O点以速度v0垂直于磁场边界及磁场方向射入磁场,经过一段时间粒子通过区域Ⅱ边界上的O'点,最终又从区域I下边界上的P点射出.图中N、P两点均未画出,但已知N点在O′点的右方,且N点与O′点相距L.区域I和Ⅱ的宽度为d=$\frac{m{v}_{0}}{2qB}$,两区域的长度足够大.N点的负电荷所带电荷量的绝对值为Q=$\frac{Lm{v}_{0}^{2}}{kq}$(其中k为静电力常量).不计粒子的重力,求:
如图所示,真空中区域I和区域Ⅱ内存在着与纸面垂直的方向相反的匀强磁场,磁感应强度大小均为B.在区域II的上边界线上的N点固定一负的点电荷,并采取措施使之只对区域II以上空间产生影响.一带正电的粒子质量为m,电荷量为q,自区域I下边界线上的O点以速度v0垂直于磁场边界及磁场方向射入磁场,经过一段时间粒子通过区域Ⅱ边界上的O'点,最终又从区域I下边界上的P点射出.图中N、P两点均未画出,但已知N点在O′点的右方,且N点与O′点相距L.区域I和Ⅱ的宽度为d=$\frac{m{v}_{0}}{2qB}$,两区域的长度足够大.N点的负电荷所带电荷量的绝对值为Q=$\frac{Lm{v}_{0}^{2}}{kq}$(其中k为静电力常量).不计粒子的重力,求: