题目内容
5.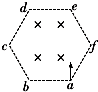 如图所示,边长为L的正六边形abcdef中,存在垂直该平面向内的匀强磁场,磁感应强度大小为B.a点处的粒子源发出大量质量为m、电荷量为+q的同种粒子,粒子的速度大小不同,方向始终垂直ab边且与磁场垂直,不计粒子的重力,当粒子的速度为v时,粒子恰好经过b点,下列说法正确的是( )
如图所示,边长为L的正六边形abcdef中,存在垂直该平面向内的匀强磁场,磁感应强度大小为B.a点处的粒子源发出大量质量为m、电荷量为+q的同种粒子,粒子的速度大小不同,方向始终垂直ab边且与磁场垂直,不计粒子的重力,当粒子的速度为v时,粒子恰好经过b点,下列说法正确的是( )| A. | 速度小于v的粒子在磁场中运动时间为$\frac{πm}{2qB}$ | |
| B. | 经过c点的粒子在磁场中做圆周运动的半径为L | |
| C. | 经过d点的粒子在磁场中运动的时间为$\frac{πm}{4qB}$ | |
| D. | 速度大于2v 小于4v的粒子一定打在cd边上 |
分析 带电粒子在磁场中做匀速圆周运动,由几何知识确定粒子的轨道半径,根据轨迹对应的圆心角分析运动时间.
解答 解:A、粒子在磁场中做匀速圆周运动,当粒子的速度为v时,粒子恰好经过b点时在磁场中运动了半周,运动时间为$\frac{1}{2}$T=$\frac{πm}{qB}$,轨迹半径等于ab的一半.当粒子的速度小于v时,由r=$\frac{mv}{qB}$知,粒子的轨迹半径小于ab的一半,仍运动半周,运动时间仍为$\frac{1}{2}$T=$\frac{πm}{qB}$,故A错误.
B、经过c点的粒子,根据几何知识知,该粒子在磁场中做圆周运动的圆心b,半径为L,故B正确.
C、在a点粒子的速度与ad连线的夹角为30°,粒子经过d点时,粒子的速度与ad连线的夹角也为30°,则粒子轨迹对应的圆心角等于60°,在磁场中运动的时间 t=$\frac{T}{6}$=$\frac{πm}{3qB}$.故C错误.
D、设经过b、c、d三点的粒子速度分别为v1、v2、v3.轨迹半径分别为r1、r2、r3.据几何知识可得,r1=$\frac{L}{2}$,r2=L,r3=2L
由半径公式r=$\frac{mv}{qB}$得:v2=2v1=2v,v3=4v1=4v,所以只有速度在这个范围:2v≤v≤4v的粒子才打在cd边上.故D正确.
故选:BD.
点评 带电粒子在匀强磁场中的运动的类型,根据题意作出粒子的运动轨迹,运用几何知识求轨迹半径,由轨迹对应的圆心角确定粒子在磁场中运动的时间是正确解题的前提与关键.

练习册系列答案
相关题目
18. 如图所示,甲、乙为竖直平面内两光滑的固定半圆形轨道,轨道甲的半径小于轨道乙,两轨道的圆心等高.a、b为两可视为质点的小球,a球质量大于b球质量.现让两球分别从轨道左端最高点由静止释放,在各自到达轨道最低点时,有( )
如图所示,甲、乙为竖直平面内两光滑的固定半圆形轨道,轨道甲的半径小于轨道乙,两轨道的圆心等高.a、b为两可视为质点的小球,a球质量大于b球质量.现让两球分别从轨道左端最高点由静止释放,在各自到达轨道最低点时,有( )
 如图所示,甲、乙为竖直平面内两光滑的固定半圆形轨道,轨道甲的半径小于轨道乙,两轨道的圆心等高.a、b为两可视为质点的小球,a球质量大于b球质量.现让两球分别从轨道左端最高点由静止释放,在各自到达轨道最低点时,有( )
如图所示,甲、乙为竖直平面内两光滑的固定半圆形轨道,轨道甲的半径小于轨道乙,两轨道的圆心等高.a、b为两可视为质点的小球,a球质量大于b球质量.现让两球分别从轨道左端最高点由静止释放,在各自到达轨道最低点时,有( )| A. | a 球的速度一定大于 b 球的速度 | |
| B. | a 球的动能一定小于 b 球的动能 | |
| C. | a 球的向心加速度一定小于 b 球的向心加速度 | |
| D. | a 球对轨道的压力一定大于 b 球对轨道的压力 |
19.下列现象中,属于光的色散现象的是( )
| A. | 雨后天空出现彩虹 | |
| B. | 通过一个狭缝观察日光灯可看到彩色条纹 | |
| C. | 海市蜃楼现象 | |
| D. | 日光照射在肥皂泡上出现彩色条纹 |
16.关于机械能,以下说法正确的是( )
| A. | 质量大的物体,重力势能一定大 | |
| B. | 速度大的物体,动能一定大 | |
| C. | 做平抛运动的物体机械能时刻在变化 | |
| D. | 质量和速率都相同的物体,动能一定相同 |
17.一个电动机,线圈电阻为0.4Ω,当它两端所加的电压为220V,通过的电流为5A的电动机每分钟所做的机械功有多少焦耳?( )
| A. | 6.54×104 | B. | 6.594×103 | C. | 1.09×104 | D. | 1.09×103 |
 如图所示,两根足够长、电阻不计且相距L=0.5m的平行金属导轨固定在倾角θ=37°的绝缘斜面上,顶端接有一个额定电压U=3V的小灯泡,两导轨间有一磁感应强度大小B=2.0T、方向垂直斜面向上的匀强磁场.今将一根长为L、质量m=0.5kg、电阻r=1.0Ω的金属棒ab垂直于导轨放置在顶端附近无初速度释放,金属棒ab与导轨始终接触良好,金属棒ab与导轨间的动摩擦因数μ=0.2,已知金属棒ab下滑到速度稳定时,小灯泡恰能正常发光,重力加速度g取10m/s2,sin 37°=0.6,cos 37°=0.8.求:
如图所示,两根足够长、电阻不计且相距L=0.5m的平行金属导轨固定在倾角θ=37°的绝缘斜面上,顶端接有一个额定电压U=3V的小灯泡,两导轨间有一磁感应强度大小B=2.0T、方向垂直斜面向上的匀强磁场.今将一根长为L、质量m=0.5kg、电阻r=1.0Ω的金属棒ab垂直于导轨放置在顶端附近无初速度释放,金属棒ab与导轨始终接触良好,金属棒ab与导轨间的动摩擦因数μ=0.2,已知金属棒ab下滑到速度稳定时,小灯泡恰能正常发光,重力加速度g取10m/s2,sin 37°=0.6,cos 37°=0.8.求: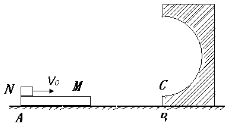 如图所示,质量为1Kg的小滑块N(可视为质点)放在质量也为1Kg的长木板M左端,N和M之间的动摩擦因数μ1=0.5,M和地面之间的动摩擦因数μ2=0.1,现给小滑块N一个水平向右的初速v0=8m/s,小滑块N和长木板M同时到达B点且此时速度大小恰好相等,小滑块到达长木板右端后,能够由C点平滑地滑上固定的光滑圆弧轨道,圆轨道半径R=0.3m,重力加速度g取10m/s2,求:
如图所示,质量为1Kg的小滑块N(可视为质点)放在质量也为1Kg的长木板M左端,N和M之间的动摩擦因数μ1=0.5,M和地面之间的动摩擦因数μ2=0.1,现给小滑块N一个水平向右的初速v0=8m/s,小滑块N和长木板M同时到达B点且此时速度大小恰好相等,小滑块到达长木板右端后,能够由C点平滑地滑上固定的光滑圆弧轨道,圆轨道半径R=0.3m,重力加速度g取10m/s2,求:
