��Ŀ����
14��ijͬѧ��ͼ��װ������֤�����غ㶨�ɣ�ʵ�鲽�����£��ٽ���ֽ����дֽ�̶�����ֱ���õ�ľ���ϣ�������¼����ľ���ײ���㣮
�ڽ�ľ����ֱ�����ڹ̶�ĩ���Ҳಢ�����Ӵ���ֻ��A���б���Ϲ��£�����A����ľ���ϵ�ײ����O�䣮
�۽�ľ��ƽ�Ƶ�ͼ����ʾλ�ã����ĩ�˲���B����A���б����ijλ���ɾ�ֹ�ͷţ��ظ�10�Σ��õ�A����ľ���ϵ�ײ�����ƽ��λ��P�䣮
��Z�ڹ��ĩ�˷���B���Խ�A���б�����ɾ�ֹ�ͷ���B����ײ���ظ�10�Σ��õ�A���B����ľ���ϵ�ײ�����ƽ��λ��M���N�䣮
ͼ��h1��h2��h3�ֱ��ʾO����N�䡢P�䡢M��ĸ߶Ȳ
��1��Ϊ��֤��������������ͬѧͨ��20�ֶȵ��α꿨��ѡ���С��ͬ������С����С��ֱ��ʱ�Ľ����ͼ�ң�����Ϊ15.20mm��
��2����ʵ������е�Ҫ������˵����ȷ����BCD
A���������⻬
B��A�����������B���
C�����ĩ�˵����߱���ˮƽ
D������ۢ��У�A��ÿ�α����б���ͬһλ���ɾ�ֹ�ͷ�
��3��ʵ���г������h1��h2��h3�⣬����Ҫ��������������B
A��A���ͷŵ㵽���ĩ�˵���ֱ�߶�h
B��A���B�������mA��mB
C�����ĩ�˵�ľ���ˮƽ����x
��4�����������������������ʽ$\frac{{m}_{A}}{\sqrt{{h}_{2}}}=\frac{{m}_{A}}{\sqrt{{h}_{3}}}+\frac{{m}_{B}}{\sqrt{{h}_{1}}}$����ʵ����������������������ű�ʾ������˵��������ײ�����ж����غ㣮

���� ��1���α꿨�ߵĶ����������߶��������α���������������
��2������ʵ���ԭ����ע������ȷ����ȷ�IJ������裮
��3��4�����ƽ���˶��Ĺ��ɣ��ó������غ�ı���ʽ���Ӷ�ȷ������Ҫ��������������
��� �⣺��1���α꿨�ߵ����߶���Ϊ15mm���α����Ϊ0.05��4mm=0.20mm�������Ϊ15.20mm��
��2��A��Ϊ�˱�֤С��A�����˵��ٶ���ȣ�ֻ�轫С��ÿ�δ�б�۵�ͬһλ���ɾ�ֹ�ͷż��ɣ�����Ҫ�⻬����A����D��ȷ��
B����������ײ���ٶȷ������ǰ����A�������������B����������B��ȷ��
C��Ϊ�˱�֤С������ij��ٶ�ˮƽ��б��ĩ�˱���ˮƽ����C��ȷ��
��ѡ��BCD��
��3��4��С��A����B��ײ��ײ��P��㣬��B����ײ��Aײ��M��㣬Bײ��N��㣬
ƽ���˶���ʱ��ֱ�Ϊ${t}_{1}=\sqrt{\frac{2{h}_{1}}{g}}$��${t}_{2}=\sqrt{\frac{2{h}_{2}}{g}}$��${t}_{3}=\sqrt{\frac{2{h}_{3}}{g}}$��
��${v}_{A}=\frac{x}{{t}_{2}}=\frac{x}{\sqrt{\frac{2{h}_{2}}{g}}}$��${v}_{A}��=\frac{x}{{t}_{3}}=\frac{x}{\sqrt{\frac{2{h}_{3}}{g}}}$��${v}_{B}=\frac{x}{{t}_{1}}=\frac{x}{\sqrt{\frac{2{h}_{1}}{g}}}$��
��mAvA=mAvA��+mBvB����$\frac{{m}_{A}}{\sqrt{{h}_{2}}}=\frac{{m}_{A}}{\sqrt{{h}_{3}}}+\frac{{m}_{B}}{\sqrt{{h}_{1}}}$��������ײ�����ж����غ㣮
��֪ʵ���г������h1��h2��h3�⣬����Ҫ��������������A���B�������mA��mB����ѡ��B��
�ʴ�Ϊ����1��15.20����2��BCD����3��B����4��$\frac{{m}_{A}}{\sqrt{{h}_{2}}}=\frac{{m}_{A}}{\sqrt{{h}_{3}}}+\frac{{m}_{B}}{\sqrt{{h}_{1}}}$��
���� ���⿼������֤�����غ㶨�ɣ�ʵ�������ӱ����α��ϵ�ʵ�鲻ͬ���������⡢��������֪��ʵ��ԭ������ȷ�����ǰ����ؼ���Ӧ��ƽ���˶����ɡ������غ㶨�����е���غ㶨�ɼ�����ȷ���⣮

| A�� | Ħ�����Թ������Ĺ�Ϊ$\frac{1}{2}$mv2 | |
| B�� | ϵͳ���ӵ�����Ϊ$\frac{1}{2}$mv2 | |
| C�� | ���ʹ���������Ĺ�Ϊ$\frac{1}{2}$mv2 | |
| D�� | ��������ڴ��ʹ�������·�̴�СΪ$\frac{{v}^{2}}{2��g}$ |
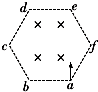 ��ͼ��ʾ���߳�ΪL����������abcdef�У����ڴ�ֱ��ƽ�����ڵ���ǿ�ų����Ÿ�Ӧǿ�ȴ�СΪB��a�㴦������Դ������������Ϊm�������Ϊ+q��ͬ�����ӣ����ӵ��ٶȴ�С��ͬ������ʼ�մ�ֱab������ų���ֱ���������ӵ������������ӵ��ٶ�Ϊvʱ������ǡ�þ���b�㣬����˵����ȷ���ǣ�������
��ͼ��ʾ���߳�ΪL����������abcdef�У����ڴ�ֱ��ƽ�����ڵ���ǿ�ų����Ÿ�Ӧǿ�ȴ�СΪB��a�㴦������Դ������������Ϊm�������Ϊ+q��ͬ�����ӣ����ӵ��ٶȴ�С��ͬ������ʼ�մ�ֱab������ų���ֱ���������ӵ������������ӵ��ٶ�Ϊvʱ������ǡ�þ���b�㣬����˵����ȷ���ǣ�������| A�� | �ٶ�С��v�������ڴų����˶�ʱ��Ϊ$\frac{��m}{2qB}$ | |
| B�� | ����c��������ڴų�����Բ���˶��İ뾶ΪL | |
| C�� | ����d��������ڴų����˶���ʱ��Ϊ$\frac{��m}{4qB}$ | |
| D�� | �ٶȴ���2v С��4v������һ������cd���� |
 ��ͼ��ʾΪ̫����·�ƣ�ÿֻ·�ƵĹ����ذ���Ч�ɹ����Լ0.3m2�����ת��Ч��ԼΪ15%������ʱ��ذ�ÿƽ���������ÿСʱ���յ���̫��������ԼΪ3.6��106J�����ÿ����Ч����ʱ��ԼΪ7h����ôÿֻ·�ƵĹ�����һ������ĵ��ܿɹ�30W ��·�ƹ���ʱ���Լ�� ��������
��ͼ��ʾΪ̫����·�ƣ�ÿֻ·�ƵĹ����ذ���Ч�ɹ����Լ0.3m2�����ת��Ч��ԼΪ15%������ʱ��ذ�ÿƽ���������ÿСʱ���յ���̫��������ԼΪ3.6��106J�����ÿ����Ч����ʱ��ԼΪ7h����ôÿֻ·�ƵĹ�����һ������ĵ��ܿɹ�30W ��·�ƹ���ʱ���Լ�� �������� ��ͼ��һ���ʵ���ԭ��Ϊ2R����һ�˹̶������Ϊ37��Ĺ̶�ֱ���AC�ĵ�A������һ��λ��ֱ�����B�������ɴ�����Ȼ״̬������Ϊm��С���P��C���ɾ�ֹ��ʼ�»���AC=7R��P��ֱ�����Ķ�Ħ��������=0.25���������ٶȴ�СΪg����ȡsin37��=0.6��cos37��=0.8��
��ͼ��һ���ʵ���ԭ��Ϊ2R����һ�˹̶������Ϊ37��Ĺ̶�ֱ���AC�ĵ�A������һ��λ��ֱ�����B�������ɴ�����Ȼ״̬������Ϊm��С���P��C���ɾ�ֹ��ʼ�»���AC=7R��P��ֱ�����Ķ�Ħ��������=0.25���������ٶȴ�СΪg����ȡsin37��=0.6��cos37��=0.8��