题目内容
5.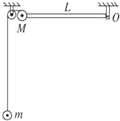 如图所示,质量为M的小球被一根长为L的可绕O轴在竖直平面内自由转动的轻质杆固定在其端点,同时又通过轻绳跨过光滑定滑轮与质量为m的小球相连.若将M由杆呈水平状态开始释放,不计摩擦,忽略杆水平时质量为M的小球与滑轮间的距离,竖直绳足够长,则杆转到竖直位置时,M、m的速度分别为多大?
如图所示,质量为M的小球被一根长为L的可绕O轴在竖直平面内自由转动的轻质杆固定在其端点,同时又通过轻绳跨过光滑定滑轮与质量为m的小球相连.若将M由杆呈水平状态开始释放,不计摩擦,忽略杆水平时质量为M的小球与滑轮间的距离,竖直绳足够长,则杆转到竖直位置时,M、m的速度分别为多大?
分析 小球M从水平位置运动到竖直位置的过程中,M、m两球组成的系统机械能守恒,M球运动到最低点,M球沿绳子方向上的分速度等于m的速度,根据系统机械能守恒求出M、m的速度.
解答 解:杆转到竖直位置时,M球下降的高度为L,绳与竖直方面成45°角,m球上升的高度为:h=$\sqrt{2}$L
设此时M球、m球的速度分别为vM、vm
根据M球沿绳子方向上的分速度等于m的速度,得:υM=$\sqrt{2}$υm
在整个运动过程中,由M、m系统的机械能守恒得:
MgL-mg•$\sqrt{2}$L=$\frac{1}{2}$MυM2+$\frac{1}{2}$mυm2
由以上三式得:υM=$\sqrt{4gl\frac{M-\sqrt{2}m}{2M+m}}$
υm=$\sqrt{2gl\frac{M-\sqrt{2}m}{2M+m}}$
答:M、m的速度分别为$\sqrt{4gl\frac{M-\sqrt{2}m}{2M+m}}$和$\sqrt{2gl\frac{M-\sqrt{2}m}{2M+m}}$.
点评 解决本题的关键知道小球m在沿绳子方向上的分速度等于M的速度,对系统研究,运用机械能守恒定律进行研究.

练习册系列答案
相关题目
16.河水的流速与船离河岸的距离的变化关系如图1所示,船在静水中的速度与时间的关系如图2所示,若要使船以最短时间渡河,则( )


| A. | 船渡河的最短时间25s | |
| B. | 船在行驶过程中,船头始终与河岸垂直 | |
| C. | 船在河水中航行的加速度大小为a=0.4m/s2 | |
| D. | 船在河水中的最大位移为156M |
13.下列关于放射性元素的半衰期的说法正确的是( )
| A. | 质量为m的铀经过两个半衰期后,原来所含的铀元素的原子核有$\frac{3}{4}$m发生了衰变 | |
| B. | 质量为m的铀经过两个半衰期后,原来所含的铀元素的原子核有$\frac{1}{4}$m发生了衰变 | |
| C. | 同种放射性元素,在化合物中的半衰期与在单质中的半衰期不相同 | |
| D. | 氡的半衰期是3.8天,若有4个氡原子核,则经过7.6天就只剩下1个氡原子核 |
17. 从距地面h高处水平抛出两个相同的小球甲和乙,不计空气阻力,球的落地点到抛出点的水平距离分别是x甲和x乙,且x甲<x乙,如图所示.则下列说法正确的是( )
从距地面h高处水平抛出两个相同的小球甲和乙,不计空气阻力,球的落地点到抛出点的水平距离分别是x甲和x乙,且x甲<x乙,如图所示.则下列说法正确的是( )
 从距地面h高处水平抛出两个相同的小球甲和乙,不计空气阻力,球的落地点到抛出点的水平距离分别是x甲和x乙,且x甲<x乙,如图所示.则下列说法正确的是( )
从距地面h高处水平抛出两个相同的小球甲和乙,不计空气阻力,球的落地点到抛出点的水平距离分别是x甲和x乙,且x甲<x乙,如图所示.则下列说法正确的是( )| A. | 甲球在空中运动的时间短 | B. | 甲、乙两球在空中运动的时间相等 | ||
| C. | 甲球平抛的初速度大 | D. | 甲、乙两球落地时速度大小相等 |
14.某振子做简谐运动的表达式为x=4sin(5πt+6π)cm,则该振子振动的振幅和周期为( )
| A. | 4cm 6πs | B. | 4cm 5πs | C. | 4cm 0.4s | D. | 以上全错 |
 如图所示,一质量为m的小球,可视为质点,系于长为R的轻绳的一端,绳的另一端固定在空间的O点,轻绳柔软且不可伸长,现把小球从O点的正上方离O点的距离为$\frac{3}{4}$R的O1点以水平速度v0=$\sqrt{\frac{2gR}{3}}$抛出.求:
如图所示,一质量为m的小球,可视为质点,系于长为R的轻绳的一端,绳的另一端固定在空间的O点,轻绳柔软且不可伸长,现把小球从O点的正上方离O点的距离为$\frac{3}{4}$R的O1点以水平速度v0=$\sqrt{\frac{2gR}{3}}$抛出.求:
 (1)木板与地面间的动摩擦因数μ;
(1)木板与地面间的动摩擦因数μ;