题目内容
8.如图所示,上表面光滑、下表面粗糙足够长质量为M=10kg的木板,在F=50N的水平拉力作用下,沿水平地面向右匀加速运动,加速度a=2.5m/s2.某时刻速度为v0=5m/s,将一个小铁块(可视为质点)无初速地放在木板最右端,这时木板恰好匀速运动,当木板运动了L=1.8m时,又将第二个同样的小铁块无初速地放在木板最右端,g取10m/s2,求: (1)木板与地面间的动摩擦因数μ;
(1)木板与地面间的动摩擦因数μ;(2)放上第二个铁块后木板又运动L距离时的速度.
分析 (1)根据牛顿第二定律求动摩擦因数;
(2)铁块放在木板上后,木板对地面的压力变大,木板受到的滑动摩擦力变大,由动能定理可以求出即将放上第二个块铁块时的速度.
解答 解:(1)木板做匀加速直线运动,由牛顿第二定律得:F-μMg=Ma
代入数据解得:μ=0.25
(2)放上第一个小铁块后木板匀速运动,由平衡条件得:F=μ(M+m)g
代入数据解得:m=10 kg
放上第二个铁块后木板又运动L距离时的速度为v,
由动能定理得:FL-μ(M+2m)gL=$\frac{1}{2}$Mv2-$\frac{1}{2}$Mv02
代入数据解得:v=4 m/s
答:(1)木板与地面间的动摩擦因数是0.25;
(2)放上第二个铁块后木板又运动L距离时的速度为4 m/s.
点评 熟练应用牛顿第二定律、动能定理即可正确解题,第(2)问也可以应用牛顿第二定律和运动学公式求解.只是有时用动能定理求解动力学问题更为简捷.

练习册系列答案
相关题目
6. 如图所示,在倾角θ=30°的光滑斜面上有一垂直于斜面的固定挡板C,质量相等的两木块A、B用一劲度系数为k的轻弹簧相连,系统处于静止状态,弹簧压缩量为l.如果用平行斜面向上的恒力F(F=mAg)拉A,当A向上运动一段距离x后撤去F,A运动到最高处B刚好不离开C,重力加速度为g,则下列说法正确的是( )
如图所示,在倾角θ=30°的光滑斜面上有一垂直于斜面的固定挡板C,质量相等的两木块A、B用一劲度系数为k的轻弹簧相连,系统处于静止状态,弹簧压缩量为l.如果用平行斜面向上的恒力F(F=mAg)拉A,当A向上运动一段距离x后撤去F,A运动到最高处B刚好不离开C,重力加速度为g,则下列说法正确的是( )
 如图所示,在倾角θ=30°的光滑斜面上有一垂直于斜面的固定挡板C,质量相等的两木块A、B用一劲度系数为k的轻弹簧相连,系统处于静止状态,弹簧压缩量为l.如果用平行斜面向上的恒力F(F=mAg)拉A,当A向上运动一段距离x后撤去F,A运动到最高处B刚好不离开C,重力加速度为g,则下列说法正确的是( )
如图所示,在倾角θ=30°的光滑斜面上有一垂直于斜面的固定挡板C,质量相等的两木块A、B用一劲度系数为k的轻弹簧相连,系统处于静止状态,弹簧压缩量为l.如果用平行斜面向上的恒力F(F=mAg)拉A,当A向上运动一段距离x后撤去F,A运动到最高处B刚好不离开C,重力加速度为g,则下列说法正确的是( )| A. | A沿斜面上升的初始加速度大小为g | B. | A上升的竖直高度最大为2l | ||
| C. | l等于x | D. | 拉力F的功率随时间均匀增加 |
3.下面列举的几种速度,其中指平均速度的是( )
| A. | 火车以76km/h的速度通过约2000m的滨州铁路大桥 | |
| B. | 汽车转弯时,速度不得超过20km/h | |
| C. | 城市某路段的路标有“15km/h、限速“字样 | |
| D. | 子弹以600m/s的速度射出枪口 |
13. 如图所示,桌面高h,质量为m的小球从距桌面高H处自由下落.假设以桌面为零势能参考面,则小球落到地面的重力势能为( )
如图所示,桌面高h,质量为m的小球从距桌面高H处自由下落.假设以桌面为零势能参考面,则小球落到地面的重力势能为( )
 如图所示,桌面高h,质量为m的小球从距桌面高H处自由下落.假设以桌面为零势能参考面,则小球落到地面的重力势能为( )
如图所示,桌面高h,质量为m的小球从距桌面高H处自由下落.假设以桌面为零势能参考面,则小球落到地面的重力势能为( )| A. | -mgh | B. | mgH | C. | mgh | D. | Mg(h+H) |
17.下述现象中说明分子之间有引力作用的是( )
| A. | 自由落体运动 | |
| B. | 磁铁能吸引小铁钉 | |
| C. | 丝绸摩擦过和玻璃棒能吸引轻小物体 | |
| D. | 两块纯净铅柱的端面刮得十分平整后用力挤压可以粘在一起 |
18.从空中以50m/s的初速度平抛一个重为10N的物体,物体在空中运动3s落地,不计空气阻力,取g=10m/s2,则物体落地时重力的瞬时功率P1、全过程的平均功率P2为( )
| A. | P1=500W P2=500W | B. | P1=300W P2=150W | ||
| C. | P1=500W P2=150W | D. | P1=700W P2=500W |
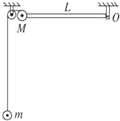 如图所示,质量为M的小球被一根长为L的可绕O轴在竖直平面内自由转动的轻质杆固定在其端点,同时又通过轻绳跨过光滑定滑轮与质量为m的小球相连.若将M由杆呈水平状态开始释放,不计摩擦,忽略杆水平时质量为M的小球与滑轮间的距离,竖直绳足够长,则杆转到竖直位置时,M、m的速度分别为多大?
如图所示,质量为M的小球被一根长为L的可绕O轴在竖直平面内自由转动的轻质杆固定在其端点,同时又通过轻绳跨过光滑定滑轮与质量为m的小球相连.若将M由杆呈水平状态开始释放,不计摩擦,忽略杆水平时质量为M的小球与滑轮间的距离,竖直绳足够长,则杆转到竖直位置时,M、m的速度分别为多大? 为了研究气体实验定律和理想气体状态方程,小强取了一根长度为L=1m的导轨性良好的直管,用胶塞将其一端封闭,使其开口向上竖直放置,向管内注放高为h=25cm的水银柱,当稳定时测出封闭的气体的长度为L1=30cm,已知外界大气压强恒为P0=75cmHg,最初外界环境的温度为t2=27℃.
为了研究气体实验定律和理想气体状态方程,小强取了一根长度为L=1m的导轨性良好的直管,用胶塞将其一端封闭,使其开口向上竖直放置,向管内注放高为h=25cm的水银柱,当稳定时测出封闭的气体的长度为L1=30cm,已知外界大气压强恒为P0=75cmHg,最初外界环境的温度为t2=27℃.