题目内容
20. 如图所示,一质量为m的小球,可视为质点,系于长为R的轻绳的一端,绳的另一端固定在空间的O点,轻绳柔软且不可伸长,现把小球从O点的正上方离O点的距离为$\frac{3}{4}$R的O1点以水平速度v0=$\sqrt{\frac{2gR}{3}}$抛出.求:
如图所示,一质量为m的小球,可视为质点,系于长为R的轻绳的一端,绳的另一端固定在空间的O点,轻绳柔软且不可伸长,现把小球从O点的正上方离O点的距离为$\frac{3}{4}$R的O1点以水平速度v0=$\sqrt{\frac{2gR}{3}}$抛出.求:(1)绳绷直后瞬间,小球的速度;
(2)当小球运动到O点的正下方时,小球的速度.
分析 (1)根据平抛运动的规律,结合几何关系,确定此时绳子刚好绷直时小球所处的位置,将该速度分解沿绳子和垂直绳方向,抓住绷紧后瞬间仅剩下垂直绳子方向的分速度求出绷紧后瞬间小球的速度.
(2)根据机械能守恒求出小球运动到O点正下方时的速度.
解答 解:小球做平抛运动.设绳即将伸直时,绳与竖直方向的夹角为θ,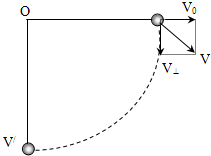
则 v0t=Rsinθ,$\frac{1}{2}g{t}^{2}=\frac{3}{4}R-Rcosθ$,
解得θ=90°,可知绳子处于水平状态时,绳子绷直,
根据h=$\frac{3}{4}R=\frac{1}{2}g{t}^{2}$得,t=$\sqrt{\frac{3R}{2g}}$,
设此时小球速度与水平方向的夹角为α,则tanα=$\frac{{v}_{y}}{{v}_{0}}=\frac{gt}{{v}_{0}}$=$\frac{\sqrt{\frac{3gR}{2}}}{\sqrt{\frac{2gR}{3}}}=\frac{3}{2}$,
将小球的速度分解为沿绳子方向和垂直绳子方向,绷直后的瞬间,仅剩下垂直绳子方向的分速度,
即v⊥=vsinα=${v}_{y}=\sqrt{\frac{3gR}{2}}$,
(2)根据机械能守恒定律得,$mgR=\frac{1}{2}m{v}^{2}-\frac{1}{2}m{{v}_{⊥}}^{2}$,
解得v=$\sqrt{\frac{7gR}{2}}$.
答:(1)绳绷直后瞬间,小球的速度为$\sqrt{\frac{3gR}{2}}$;
(2)当小球运动到O点的正下方时,小球的速度为$\sqrt{\frac{7gR}{2}}$.
点评 本题关键是将小球的运动分为三个过程进行分析讨论,平抛运动过程、突然绷紧的瞬时过程和变速圆周运动过程;然后根据对各段运用平抛运动位移公式、速度分解法则、机械能守恒定律进行求解,有一定的难度.

| A. | X射线的波长比紫外线的波长更长 | |
| B. | 在水中各种电磁波的传播速度均相同 | |
| C. | 电磁波和机械波都能发生干涉和衍射现象 | |
| D. | 麦克斯韦在人类历史上首先捕捉到了电磁波 |
 如图所示,粗糙水平轨道AB与竖直平面内的光滑半圆轨道BDC在B处相切,B、C分别为半圆轨道的最低点和最高点,一个质量为m的物块P(可视为质点)被一根细线拴住放在水平轨道上,细线的左端固定在竖直墙壁上,墙壁和物块P之间夹一根被压缩的轻弹簧,此时P到B点的距离为x0.现将细线剪断,物块P被弹簧向右弹出后滑上半圆轨道,恰好能通过C点,最后落回水平轨道上的E点(题中未画出).物块P与水平轨道间的摩擦因数为μ,半圆轨道的半径为R,空气阻力不计,重力加速度为g,求:
如图所示,粗糙水平轨道AB与竖直平面内的光滑半圆轨道BDC在B处相切,B、C分别为半圆轨道的最低点和最高点,一个质量为m的物块P(可视为质点)被一根细线拴住放在水平轨道上,细线的左端固定在竖直墙壁上,墙壁和物块P之间夹一根被压缩的轻弹簧,此时P到B点的距离为x0.现将细线剪断,物块P被弹簧向右弹出后滑上半圆轨道,恰好能通过C点,最后落回水平轨道上的E点(题中未画出).物块P与水平轨道间的摩擦因数为μ,半圆轨道的半径为R,空气阻力不计,重力加速度为g,求: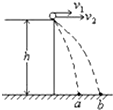 从高为h=10m的平台上,分两次沿同一方向水平抛出一个质量m=5kg的小球.如图所示,第一次小球在a点落地.第二次小球在b点落地,ab相距为d=3m.已知第一次抛球的初速度为v1=2m/s,(g取9.8m/s2)求:
从高为h=10m的平台上,分两次沿同一方向水平抛出一个质量m=5kg的小球.如图所示,第一次小球在a点落地.第二次小球在b点落地,ab相距为d=3m.已知第一次抛球的初速度为v1=2m/s,(g取9.8m/s2)求: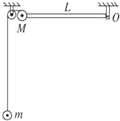 如图所示,质量为M的小球被一根长为L的可绕O轴在竖直平面内自由转动的轻质杆固定在其端点,同时又通过轻绳跨过光滑定滑轮与质量为m的小球相连.若将M由杆呈水平状态开始释放,不计摩擦,忽略杆水平时质量为M的小球与滑轮间的距离,竖直绳足够长,则杆转到竖直位置时,M、m的速度分别为多大?
如图所示,质量为M的小球被一根长为L的可绕O轴在竖直平面内自由转动的轻质杆固定在其端点,同时又通过轻绳跨过光滑定滑轮与质量为m的小球相连.若将M由杆呈水平状态开始释放,不计摩擦,忽略杆水平时质量为M的小球与滑轮间的距离,竖直绳足够长,则杆转到竖直位置时,M、m的速度分别为多大?
 如图所示,将小球从斜面的顶点处平抛出去,且能落在斜面上.已知抛出时速度大小为v0,斜面与水平方向的夹角为θ.在小球运动过程中距离斜面最远时,其速度大小为$\frac{{v}_{0}}{cosθ}$,小球从抛出到该时所用时间为$\frac{{v}_{0}tanθ}{g}$.
如图所示,将小球从斜面的顶点处平抛出去,且能落在斜面上.已知抛出时速度大小为v0,斜面与水平方向的夹角为θ.在小球运动过程中距离斜面最远时,其速度大小为$\frac{{v}_{0}}{cosθ}$,小球从抛出到该时所用时间为$\frac{{v}_{0}tanθ}{g}$.