��Ŀ����
13��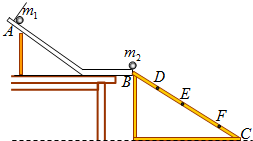 Ϊ����֤��ײ�еĶ����غ�ͼ�������С�����ײ�Ƿ�Ϊ������ײ����ײ������û�л�е����ʧ����ijͬѧѡȡ�����������ͬ����������ȵ�С������������������ʵ�飺
Ϊ����֤��ײ�еĶ����غ�ͼ�������С�����ײ�Ƿ�Ϊ������ײ����ײ������û�л�е����ʧ����ijͬѧѡȡ�����������ͬ����������ȵ�С������������������ʵ�飺A������ƽ�������С��������ֱ�Ϊm1��m2����m1��m2��
B��������ͼ��ʾ����������װ��ʵ��װ�ã���б��AB�̶������ߣ�ʹ�۵�ĩ�˵������ˮƽ����һб��BC������б��ĩ�ˣ�
C���Ȳ���С��m2����С��m1��б�۶���A���ɾ�ֹ��ʼ���£�����С����б���ϵ����λ�ã�
D����С��m2����б��ǰ�˱�Ե�ϣ���С��m1��б�۶���A�����£�ʹ���Ƿ�����ײ������С��m1��С��m2��б���ϵ����λ�ã�
D���ú��̶ȳ������������λ�õ�б��ĩ�˵�B�ľ��룮ͼ��D��E��F���Ǹ�ͬѧ���µ�С����б���ϵļ������λ�ã���B��ľ���ֱ�ΪLD��LE��LF��
���ݸ�ͬѧ��ʵ�飬����ش��������⣺
��1��С��m1��m2������ײ��m1�������ͼ�е�D�㣬m2�������ͼ�е�F�㣮
��2���ò�õ�����������ʾ��ֻҪ�����ϵʽm1$\sqrt{{L}_{E}}$=m1$\sqrt{{L}_{D}}$+m2$\sqrt{{L}_{F}}$����˵����ײ�ж������غ�ģ�
��3���ò�õ�����������ʾ��ֻҪ�������ϵʽm1LE=m1LD+m2LF����˵����С�����ײ�ǵ�����ײ��
���� ��1��С��m1��С��m2��ײ��С��m2���ٶ�����С��m1���ٶȼ�С������ƽ���˶�����ƽ���˶����ɲ����жϳ���
��2����б��BC��ˮƽ������Ϊ������ƽ���˶����������ײǰ��С��m1��С��m2���ٶȣ���ʾ�������ı���ʽ������⣻
��3������С�����ײ�ǵ�����ײ������ײǰ���е��û����ʧ�����ݻ�е���غ㶨�ɿ���ñ���ʽ��
��� �⣺��1��С��m1��С��m2��ײ��С��m2���ٶ�����С��m1���ٶȼ�С������ƽ���˶���������ײ��m1�����ص���D�㣬m2�����ص���F�㣻
��2����ײǰ��С��m1����ͼ�е�E�㣬����ˮƽ���ٶ�Ϊv1��С��m1��m2������ײ��m1�������ͼ�е�D�㣬����ˮƽ���ٶ�Ϊv1�䣬m2�������ͼ�е�F�㣬����ˮƽ���ٶ�Ϊv2�� ��б��BC��ˮƽ������Ϊ����
��ƽ���˶����ɵã�LDsin��=$\frac{1}{2}$gt2��LDcos��=v��1t
��ã�v��1=$\sqrt{\frac{g{L}_{D}��cos����^{2}}{2sin��}}$
ͬ���ɽ�ã�v1=$\sqrt{\frac{g{L}_{E}��cos����^{2}}{2sin��}}$��v2=$\sqrt{\frac{g{L}_{F}��cos����^{2}}{2sin��}}$
����ֻҪ����m1v1=m2v2+m1v��1
����m1$\sqrt{{L}_{E}}$=m1$\sqrt{{L}_{D}}$+m2$\sqrt{{L}_{F}}$�� ��˵��������ײ�����ж����غ㣻
��3������С�����ײ�ǵ�����ײ������ײǰ���е��û����ʧ����Ҫ�����ϵʽ
$\frac{1}{2}$m1v12=$\frac{1}{2}$m1v��12+$\frac{1}{2}$m2v2
��m1LE=m1LD+m2LF
�ʴ�Ϊ����1��D��F
��2��m1$\sqrt{{L}_{E}}$=m1$\sqrt{{L}_{D}}$+m2$\sqrt{{L}_{F}}$
��3��m1LE=m1LD+m2LF
���� ��������ƽ���˶��Ĺ��ɿ��鶯���غ㶨�ɵ���֤����Ŀ��Ϊ��ӱ��Ҫѧ������ƽ���˶��Ļ������������ײǰ����ٶȣ��Ӷ���֤�����غ㶨�ɣ�ͬʱע����С�����ײ�ǵ�����ײ������ײǰ���е��û����ʧ��

 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�| A�� | ��ʽ��GΪ��������������ţ�ٲ��������� | |
| B�� | R��������ʱ������������������� | |
| C�� | m1��m2֮��������������Ǵ�С��ȣ���m1��m2�������Ƿ������ | |
| D�� | m1��m2֮��������������Ǵ�С��ȷ����෴����һ��ƽ���� |
 һ������Ȧ����ǿ�ų�������ת������������ʽ�����磬����Ȧƽ����������ʱ����ͼ��ʾ��������˵������ȷ���ǣ�������
һ������Ȧ����ǿ�ų�������ת������������ʽ�����磬����Ȧƽ����������ʱ����ͼ��ʾ��������˵������ȷ���ǣ�������| A�� | ͨ����Ȧ�ĸ�Ӧ�綯��Ϊ�� | B�� | ��ͨ���ı仯�ʴﵽ���ֵ | ||
| C�� | ͨ����Ȧ�Ĵ�ͨ���ﵽ���ֵ | D�� | ͨ����Ȧ�ĸ�Ӧ����Ϊ�� |
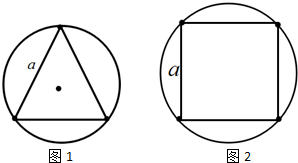
 ͼʾΪһ��������ݣ�a��b��c�������ϵ������㣮�������ƴ�ֱ�ڵ���������Խ��ٶȦ��ȶ���תʱ�����б�����ȷ���ǣ�������
ͼʾΪһ��������ݣ�a��b��c�������ϵ������㣮�������ƴ�ֱ�ڵ���������Խ��ٶȦ��ȶ���תʱ�����б�����ȷ���ǣ�������| A�� | a��b�Ľ��ٶȱ�c�Ĵ� | B�� | c�����ٶȱ�a��b�Ĵ� | ||
| C�� | a��b��c��������ٶȴ�С��� | D�� | a��b��c����Ľ��ٶ���� |
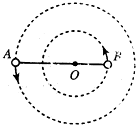 ����ĺڶ��ǽ�������������Ԥ�Ե�һ���������壬̽Ѱ�ڶ��ķ���֮һ�ǹ۲�˫��ϵͳ���˶����ɣ�����ѧ�ҹ۲������ϵ����������ʱ��������LMCX-3˫��ϵͳ�����ɿɼ���A�Ͳ��ɼ��İ���B���ɣ�������Ϊ�ʵ㣬���������������Ӱ�죬A��BΧ�����������ϵ�O��������Բ���˶�������֮��ľ��뱣�ֲ��䣬��ͼ��ʾ����������ΪG���ɹ۲��ܹ��õ��ɼ���A������v����������T��
����ĺڶ��ǽ�������������Ԥ�Ե�һ���������壬̽Ѱ�ڶ��ķ���֮һ�ǹ۲�˫��ϵͳ���˶����ɣ�����ѧ�ҹ۲������ϵ����������ʱ��������LMCX-3˫��ϵͳ�����ɿɼ���A�Ͳ��ɼ��İ���B���ɣ�������Ϊ�ʵ㣬���������������Ӱ�죬A��BΧ�����������ϵ�O��������Բ���˶�������֮��ľ��뱣�ֲ��䣬��ͼ��ʾ����������ΪG���ɹ۲��ܹ��õ��ɼ���A������v����������T�� ��ͼ��ʾ�������ƽ̨�Ϸ���һ���壬����ӵ������պ�����ֱ���ϵ��ȼ����˶������ٶȴ�СΪ$\frac{g}{3}$��������ijһ�߶�ʱ�������ƽ̨��ѹ����СΪ���ǰѹ����$\frac{4}{9}$����֪����뾶ΪR��������ʱ�����ĸ߶ȣ���gΪ������������ٶȣ�
��ͼ��ʾ�������ƽ̨�Ϸ���һ���壬����ӵ������պ�����ֱ���ϵ��ȼ����˶������ٶȴ�СΪ$\frac{g}{3}$��������ijһ�߶�ʱ�������ƽ̨��ѹ����СΪ���ǰѹ����$\frac{4}{9}$����֪����뾶ΪR��������ʱ�����ĸ߶ȣ���gΪ������������ٶȣ�