题目内容
8. 如图所示,火箭的平台上放有一物体,火箭从地面升空后,做竖直向上的匀加速运动,加速度大小为$\frac{g}{3}$,上升到某一高度时,物体对平台的压力减小为起飞前压力的$\frac{4}{9}$.已知地球半径为R,求火箭此时离地面的高度.(g为地面的重力加速度)
如图所示,火箭的平台上放有一物体,火箭从地面升空后,做竖直向上的匀加速运动,加速度大小为$\frac{g}{3}$,上升到某一高度时,物体对平台的压力减小为起飞前压力的$\frac{4}{9}$.已知地球半径为R,求火箭此时离地面的高度.(g为地面的重力加速度)
分析 以测试仪器为研究对象,根据牛顿第二定律求出某一高度处的重力加速度,再由重力等于万有引力,应用比例法求解火箭离地面的高度.
解答 解:取测试仪为研究对象,由物体的平衡条件有:
起飞前:FN1=mg0
在某一高度处:${F}_{N2}-m{g}_{2}=ma=m\frac{g}{3}$
高h处的万有引力:mg2=$\frac{GMm}{(R+h)^{2}}$
地面处的万有引力:mg0=$\frac{GMm}{{R}^{2}}$
由题意知$\frac{{F}_{N2}}{{F}_{{N}_{1}}}$=$\frac{4}{9}$,
联立解得:h=2R
答:火箭此时离地面的高度是2R.
点评 本题中g=$\frac{GM}{(R+h)^{2}}$称为黄金代换式,反映了重力加速度与高度的关系,可根据重力与万有引力推导出来的.

练习册系列答案
相关题目
19.如图所示,在外力作用下某质点运动的v-t图象为正弦曲线,从图中可以判断( )

| A. | 在t2时刻,外力的功率最大 | |
| B. | 在0-t1时间内,外力做正功 | |
| C. | 在0-t1时间内,外力的功率逐渐增大 | |
| D. | 在t1-t2时间内,外力做的总功为零 |
16.质量相同的两方形木块A、B紧靠一起放在光滑水平面上,一子弹先后水平穿透两木块后射出,若木块对子弹的阻力恒定不变,且子弹射穿两木块的时间相同,则子弹射穿木块时A、B木块的速度之比( )
| A. | 1:1 | B. | 1:2 | C. | 1:3 | D. | 1:$\sqrt{2}$ |
3.当忽略地球自转时,地表处的重力加速度和在地表上空处的重力加速度均由地球对物体的万有引力产生.设地球是一个近似球体,地球的半径为R,地表处的重力加速度为g0,物体在距离地球表面4R高度处的重力加速度为g,则$\frac{g}{{g}_{0}}$为( )
| A. | 1 | B. | $\frac{1}{4}$ | C. | $\frac{1}{5}$ | D. | $\frac{1}{25}$ |
20.如图所示,甲、乙、丙三个光滑斜面,它们的高度相同、倾角不同,θ1<θ1<θ3.现让完全相同的物块沿斜面由静止从顶端运动到底端.关于物块沿不同斜面运动时重力做功W和重力做功的平均功率P,下列说法正确的是( )


| A. | W甲<W乙<W丙 | B. | P甲>P乙>P丙 | C. | W甲=W乙=W丙 | D. | P甲<P乙<P丙 |
17.下列哪种桥损害程度最小( )
| A. | 直 桥 | B. | 拱形桥 | C. | 凹形桥 | D. | 没有区别 |
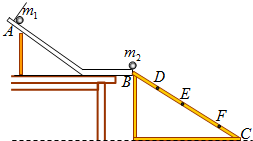 为了验证碰撞中的动量守恒和检验两个小球的碰撞是否为弹性碰撞(碰撞过程中没有机械能损失),某同学选取了两个体积相同、质量不相等的小球,按下述步骤做了如下实验:
为了验证碰撞中的动量守恒和检验两个小球的碰撞是否为弹性碰撞(碰撞过程中没有机械能损失),某同学选取了两个体积相同、质量不相等的小球,按下述步骤做了如下实验: