题目内容
4.发电机的输出电压为220V,输出功率为44KW,输电线总电阻为0.4Ω,发电站先用变压比为1:10的升压变压器将电压升高,经同样输电线路后,再经过10:1的降压变压器降压后供给用户,求:(1)输电线上电流为多少;
(2)输电线上损失的功率为多少;
(3)用户端的功率为多少;
(4)用户端的电压多少.
分析 根据升压变压器原副线圈的匝数比和输入电压,求出输出电压,从而得出输送的电流,根据P损=I2R求出输电线上损耗的功率.根据输电线上的电压损失得出降压变压器的输入电压,从而得出用户得到的电压.根据功率损失求出用户得到的功率
解答 解:(1)如果用1:10的变压器将电压升高到2200V后再输送出去,则输出电流为:
$I=\frac{P}{{U}_{2}}=\frac{44000}{2200}A=20A$?
?(2)?输电线上损失功率△P=I2r=202×0.4W=160W
(3)用户得到的电功率为P用=P-△P=43.84kW
?(4)?在导线上损失的电压为:△U=Ir=20V×0.4Ω=8V
??加到用户端变压器上的电压为:U=U2-△U=2192V
根据电压与匝数成正比得用户得到的电压为:U4=$\frac{U}{10}$=219.6V;
答:(1)输电线上电流为20A;
(2)输电线上损失的功率为160W;
(3)用户端的功率为43.84kW;
(4)用户端的电压219.6V.
点评 本题的关键:1、原副线圈的电压比、电流比与匝数比的关系;2、输送功率、输送电压、电流的关系

练习册系列答案
相关题目
14.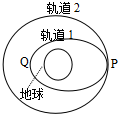 2008年9月25日至28日我国成功实施了“神舟”七号载人航天飞行并实现了航天员首次出舱.飞船先沿椭圆轨道飞行,后在远地点343千米处点火加速,由椭圆轨道变成高度为343千米的圆轨道,在此圆轨道上飞船运行周期约为90分钟.下列判断正确的是( )
2008年9月25日至28日我国成功实施了“神舟”七号载人航天飞行并实现了航天员首次出舱.飞船先沿椭圆轨道飞行,后在远地点343千米处点火加速,由椭圆轨道变成高度为343千米的圆轨道,在此圆轨道上飞船运行周期约为90分钟.下列判断正确的是( )
 2008年9月25日至28日我国成功实施了“神舟”七号载人航天飞行并实现了航天员首次出舱.飞船先沿椭圆轨道飞行,后在远地点343千米处点火加速,由椭圆轨道变成高度为343千米的圆轨道,在此圆轨道上飞船运行周期约为90分钟.下列判断正确的是( )
2008年9月25日至28日我国成功实施了“神舟”七号载人航天飞行并实现了航天员首次出舱.飞船先沿椭圆轨道飞行,后在远地点343千米处点火加速,由椭圆轨道变成高度为343千米的圆轨道,在此圆轨道上飞船运行周期约为90分钟.下列判断正确的是( )| A. | 飞船在轨道1的运行周期大于在轨道2的运行周期 | |
| B. | 飞船在圆轨道上时航天员出舱前后都处于失重状态 | |
| C. | 飞船在此圆轨道上运动的角度速度大于同步卫星运动的角速度 | |
| D. | 飞船变轨前通过椭圆轨道远地点时的加速度大于变轨后沿圆轨道运动的加速度 |
19.如图所示,在外力作用下某质点运动的v-t图象为正弦曲线,从图中可以判断( )

| A. | 在t2时刻,外力的功率最大 | |
| B. | 在0-t1时间内,外力做正功 | |
| C. | 在0-t1时间内,外力的功率逐渐增大 | |
| D. | 在t1-t2时间内,外力做的总功为零 |
9.太空中存在一些离其它恒星较远的、由质量相等的三颗星组成的三星系统,通常可忽略其它星体对它们的引力作用.已观测到稳定的三星系统存在两种基本的构成形式:一种是三颗星位于同一直线上,两颗星围绕中央星在同一半径为R的圆轨道上运行;另一种形式是三颗星位于等边三角形的三个顶点上,并沿外接于等边三角形的圆形轨道运行.设这三个星体的质量均为M,并设两种系统的运动周期相同,则下列说法不正确的是( )


| A. | 直线三星系统中甲星和丙星的角速度相同 | |
| B. | 此三星系统的运动周期为T=4πR$\sqrt{\frac{R}{5GM}}$ | |
| C. | 三角形三星系统中星体间的距离为L=$\root{3}{{\frac{12}{5}}}$R | |
| D. | 三角形三星系统的线速度大小为$\frac{1}{2}$$\sqrt{\frac{5GM}{R}}$ |
16.质量相同的两方形木块A、B紧靠一起放在光滑水平面上,一子弹先后水平穿透两木块后射出,若木块对子弹的阻力恒定不变,且子弹射穿两木块的时间相同,则子弹射穿木块时A、B木块的速度之比( )
| A. | 1:1 | B. | 1:2 | C. | 1:3 | D. | 1:$\sqrt{2}$ |
14. 如图所示,导线框abcd与导线在同一平面内,直导线通恒定电流I,当线框由左向右匀速运动到虚线框的过程,线框中感应电流方向是( )
如图所示,导线框abcd与导线在同一平面内,直导线通恒定电流I,当线框由左向右匀速运动到虚线框的过程,线框中感应电流方向是( )
 如图所示,导线框abcd与导线在同一平面内,直导线通恒定电流I,当线框由左向右匀速运动到虚线框的过程,线框中感应电流方向是( )
如图所示,导线框abcd与导线在同一平面内,直导线通恒定电流I,当线框由左向右匀速运动到虚线框的过程,线框中感应电流方向是( )| A. | 先abcd,后dcba,再abcd | B. | 先abcd,后dcba | ||
| C. | 始终沿dcba | D. | 先dcba,后abcd,再dcba |
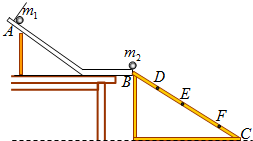 为了验证碰撞中的动量守恒和检验两个小球的碰撞是否为弹性碰撞(碰撞过程中没有机械能损失),某同学选取了两个体积相同、质量不相等的小球,按下述步骤做了如下实验:
为了验证碰撞中的动量守恒和检验两个小球的碰撞是否为弹性碰撞(碰撞过程中没有机械能损失),某同学选取了两个体积相同、质量不相等的小球,按下述步骤做了如下实验: