题目内容
3.宇宙中存在一些离其他恒星较远的、由质量均为m四颗星组成的四星系统,通常可忽略其他星体对它们的引力作用,已知稳定的四星系统存在一种形式是(如图1所示):三颗星位于等边三角形的三个顶点上,第四颗位于其中心,三个顶点上三颗星沿外接等边三角形的圆形轨道运行,等边三角形边长为a,引力常量为G.求: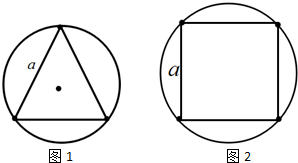
(1)顶点上星体做匀速圆周运动的轨道半径R1;
(2)等边三角形顶点上星体受的合力F1;
(3)三颗星沿外接等边三角形的圆形轨道运行周期T1;
(4)已知稳定的四星系统存在另一种形式是(如图2所示):四颗星位于正方形的四个顶点上,四颗星均围绕正方形的中心做匀速圆周运动,正方形边长为a.四颗星围绕正方形中心做匀速圆周运动周期T2.请判断T1和T2的大小,并说出你判断的理由.
分析 (1)结合几何关系即可求出顶点上星体做匀速圆周运动的轨道半径R1;
(2)根据万有引力定律,结合矢量合成的方法即可求出等边三角形顶点上星体受的合力F1;
(3)明确研究对象,对研究对象受力分析,找到做圆周运动所需向心力的来源.在四颗星组成的四星系统中,其中任意一颗星受到其它三颗星对它的合力提供圆周运动的向心力,根据F合=mr($\frac{2π}{T}$)2,求出星体匀速圆周运动的周期.
(4)同(3)的方法求出周期,然后比较即可.
解答 解:(1)对三绕一模式,等边三角形边长为a,三颗绕行星轨道半径均为r,由几何关系得三角形的边长为a=$\sqrt{3}$r,即r1=$\frac{\sqrt{3}}{3}$a,
(2)根据矢量合成的方法可得:${F}_{1}=2•\frac{{Gm}^{2}}{{a}^{2}}cos30°+G\frac{{m}^{2}}{{r}_{1}^{2}}$=$\frac{(3+\sqrt{3})G{m}^{2}}{{a}^{2}}$
(3)由所受合力等于向心力得
$\frac{(3+\sqrt{3})G{m}^{2}}{{a}^{2}}=m\frac{4{π}^{2}}{{{T}_{2}}^{2}}{r}_{1}$
解得:T1=$2π\sqrt{\frac{(3-\sqrt{3}){a}^{3}}{2Gm}}$
(4)对于第二种形式:
星体在其他三个星体的万有引力作用下围绕正方形对角线的交点做匀速圆周运动,其轨道半径半径r1=$\frac{\sqrt{2}}{2}a$
由万有引力定律和向心力公式得:$\frac{G{m}^{2}}{2{a}^{2}}+2\frac{G{m}^{2}}{{a}^{2}}$cos45°=m${r}_{1}\frac{4{π}^{2}}{{{T}_{1}}^{2}}$
解得:T1=2πa$\sqrt{\frac{2a}{(4+\sqrt{2})Gm}}$
联立得:$\frac{{T}_{1}}{{T}_{2}}$=$\sqrt{\frac{(4-\sqrt{2})(3+\sqrt{3})}{21}}$≈$\sqrt{0.58}$<1
答:(1)顶点上星体做匀速圆周运动的轨道半径是$\frac{\sqrt{3}}{3}$a;
(2)等边三角形顶点上星体受的合力F1是$\frac{(3+\sqrt{3})G{m}^{2}}{{a}^{2}}$;
(3)三颗星沿外接等边三角形的圆形轨道运行周期T1是$2π\sqrt{\frac{(3-\sqrt{3}){a}^{3}}{2Gm}}$;
(4)已知稳定的四星系统存在另一种形式是(如图2所示):四颗星位于正方形的四个顶点上,四颗星均围绕正方形的中心做匀速圆周运动,正方形边长为a.四颗星围绕正方形中心做匀速圆周运动周期T2.则T1小于T2的大小.
点评 知道在四颗星组成的四星系统中,其中任意一颗星受到其它三颗星对它的合力提供圆周运动的向心力.
万有引力定律和牛顿第二定律是力学的重点,在本题中有些同学找不出什么力提供向心力,关键在于进行正确受力分析.

| A. | 若它们的初动能相同,则甲物体运动的时间较长 | |
| B. | 若它们的初动能相同,则乙物体运动的时间较长 | |
| C. | 若它们的初动量相同,则甲物体运动的时间较长 | |
| D. | 若它们的初动量相同,则乙物体运动的时间较长 |
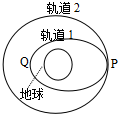 2008年9月25日至28日我国成功实施了“神舟”七号载人航天飞行并实现了航天员首次出舱.飞船先沿椭圆轨道飞行,后在远地点343千米处点火加速,由椭圆轨道变成高度为343千米的圆轨道,在此圆轨道上飞船运行周期约为90分钟.下列判断正确的是( )
2008年9月25日至28日我国成功实施了“神舟”七号载人航天飞行并实现了航天员首次出舱.飞船先沿椭圆轨道飞行,后在远地点343千米处点火加速,由椭圆轨道变成高度为343千米的圆轨道,在此圆轨道上飞船运行周期约为90分钟.下列判断正确的是( )| A. | 飞船在轨道1的运行周期大于在轨道2的运行周期 | |
| B. | 飞船在圆轨道上时航天员出舱前后都处于失重状态 | |
| C. | 飞船在此圆轨道上运动的角度速度大于同步卫星运动的角速度 | |
| D. | 飞船变轨前通过椭圆轨道远地点时的加速度大于变轨后沿圆轨道运动的加速度 |
| A. | 牛顿是在开普勒揭示的行星运动规律的基础上,发现了万有引力定律,因此万有引力定律仅适用于天体之间 | |
| B. | 万有引力定律对质量大的物体适用,对质量小的物体不适用 | |
| C. | 由公式F=$\frac{G{m}_{1}{m}_{2}}{{r}^{2}}$可知,当两物体间的距离r趋于零时,万有引力趋于无穷大 | |
| D. | 卡文迪许首先用实验比较准确地测定了引力常量G的数值 |
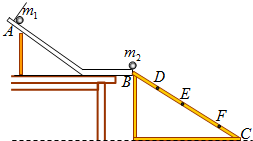 为了验证碰撞中的动量守恒和检验两个小球的碰撞是否为弹性碰撞(碰撞过程中没有机械能损失),某同学选取了两个体积相同、质量不相等的小球,按下述步骤做了如下实验:
为了验证碰撞中的动量守恒和检验两个小球的碰撞是否为弹性碰撞(碰撞过程中没有机械能损失),某同学选取了两个体积相同、质量不相等的小球,按下述步骤做了如下实验: