题目内容
20.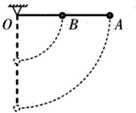 如图所示,一长为L的轻质细杆可绕其一端O点在竖直平面内自由转动,在杆的中点和另一端分别固定两个质量相等的可看作质点的A、B小球.重力加速度为g,不计空气阻力.现将杆从水平位置静止释放,下列说法正确的是( )
如图所示,一长为L的轻质细杆可绕其一端O点在竖直平面内自由转动,在杆的中点和另一端分别固定两个质量相等的可看作质点的A、B小球.重力加速度为g,不计空气阻力.现将杆从水平位置静止释放,下列说法正确的是( )| A. | A球机械能守恒 | |
| B. | A球运动到最低点时,重力的功率为零 | |
| C. | A球到达最低点时的速度为2$\sqrt{\frac{3gL}{5}}$ | |
| D. | 以后A球一定能回到释放点 |
分析 对A、B两球组成的系统,在运动的过程中只有重力做功,系统机械能守恒,抓住A、B的角速度相等,根据A、B的速度关系,利用系统机械能守恒定律求出A、B两球的速度.
解答 解:A、设当杆转到竖直位置时,A球和B球的速度分别为vA和vB.如果把轻杆、两球组成的系统作为研究对象,系统机械能守恒,拉力对A做负功,机械能减小,故A错误.
B、根据P=FVcosθ知最低点重力和速度垂直,故功率为零,故B正确;
C、若取B的最低点为重力势能参考平面,根据△E减=△E增
可得:mgL+$\frac{1}{2}$mgL=$\frac{1}{2}$mv${\;}_{A}^{2}$+$\frac{1}{2}$mv${\;}_{B}^{2}$
又因A球与B球在各个时刻对应的角速度相同,故vA=2vB
由以上二式得:vA=$\sqrt{\frac{3gL}{5}}$,故C正确;
D、根据能量守恒定律知A可以回到释放点,故D正确;
故选:BCD
点评 解决本题的关键知道A、B两球在运动的过程中,系统机械能守恒,求出A、B的速度,注意单个小球机械能不守恒.

练习册系列答案
 期末集结号系列答案
期末集结号系列答案
相关题目
10. 一理想自耦变压器的原线圈接有正弦交变电压如图甲所示,副线圈接有可调电阻R,触头P与线圈始终接触良好,如图乙所示,下列判断正确的是( )
一理想自耦变压器的原线圈接有正弦交变电压如图甲所示,副线圈接有可调电阻R,触头P与线圈始终接触良好,如图乙所示,下列判断正确的是( )
 一理想自耦变压器的原线圈接有正弦交变电压如图甲所示,副线圈接有可调电阻R,触头P与线圈始终接触良好,如图乙所示,下列判断正确的是( )
一理想自耦变压器的原线圈接有正弦交变电压如图甲所示,副线圈接有可调电阻R,触头P与线圈始终接触良好,如图乙所示,下列判断正确的是( )| A. | 交变电源的电压u随时间t变化的规律是u=U0cos(100πt)V | |
| B. | 若仅将触头P向A端滑动,则电阻R消耗的电功率增大 | |
| C. | 若仅使电阻R增大,则原线圈的输入电功率增大 | |
| D. | 若使电阻R增大的同时,将触头P向B端滑动,则通过A处的电流一定增大 |
15. 如图所示,小球在竖直向下的力F作用下,将竖直轻弹簧压缩,若将力F撤去,小球将向上弹起并离开弹簧直到速度为零.在小球向上运动的整个过程中,下列说法正确的是( )
如图所示,小球在竖直向下的力F作用下,将竖直轻弹簧压缩,若将力F撤去,小球将向上弹起并离开弹簧直到速度为零.在小球向上运动的整个过程中,下列说法正确的是( )
 如图所示,小球在竖直向下的力F作用下,将竖直轻弹簧压缩,若将力F撤去,小球将向上弹起并离开弹簧直到速度为零.在小球向上运动的整个过程中,下列说法正确的是( )
如图所示,小球在竖直向下的力F作用下,将竖直轻弹簧压缩,若将力F撤去,小球将向上弹起并离开弹簧直到速度为零.在小球向上运动的整个过程中,下列说法正确的是( )| A. | 小球的动能先增大后减小 | |
| B. | 小球的机械能守恒,小球和弹簧组成的系统机械能不守恒 | |
| C. | 小球离开弹簧时动能最大 | |
| D. | 小球动能最大时弹性势能不为零 |
12. 一个内壁光滑的圆锥形筒的轴线垂直水平面,圆锥筒固定,有质量相等的小球A和B沿着筒的内壁在水平面内做匀速圆周运动,A的运动半径较大,则( )
一个内壁光滑的圆锥形筒的轴线垂直水平面,圆锥筒固定,有质量相等的小球A和B沿着筒的内壁在水平面内做匀速圆周运动,A的运动半径较大,则( )
 一个内壁光滑的圆锥形筒的轴线垂直水平面,圆锥筒固定,有质量相等的小球A和B沿着筒的内壁在水平面内做匀速圆周运动,A的运动半径较大,则( )
一个内壁光滑的圆锥形筒的轴线垂直水平面,圆锥筒固定,有质量相等的小球A和B沿着筒的内壁在水平面内做匀速圆周运动,A的运动半径较大,则( )| A. | 球A的线速度小于球B的线速度 | B. | 球A与球B对筒壁的压力相等 | ||
| C. | 球A的运动周期小于球B的运动周期 | D. | 球A的加速度小于球B的加速度 |
 如图所示,放在斜面上重力为10N的物体在水平推力F=20N的作用下,沿斜面匀速上滑.已知斜面倾斜角为α=37°.(sin37°=0.6,cos37°=0.8)问:
如图所示,放在斜面上重力为10N的物体在水平推力F=20N的作用下,沿斜面匀速上滑.已知斜面倾斜角为α=37°.(sin37°=0.6,cos37°=0.8)问:

 如图所示,真空中有一块直角三角形的玻璃砖ABC,∠B=30°,若CA的延长线上S点有一点光源发出的一条光线由D点射入玻璃砖,光线经玻璃砖折射后垂直BC边射出,且此光束从S 传播到D的时间与在玻璃砖内的传播时间相等,已知光在真空中的传播速度为c,BD=$\sqrt{2}$d,∠ASD=15°.求:
如图所示,真空中有一块直角三角形的玻璃砖ABC,∠B=30°,若CA的延长线上S点有一点光源发出的一条光线由D点射入玻璃砖,光线经玻璃砖折射后垂直BC边射出,且此光束从S 传播到D的时间与在玻璃砖内的传播时间相等,已知光在真空中的传播速度为c,BD=$\sqrt{2}$d,∠ASD=15°.求: