题目内容
9.“北斗”卫星导航定位系统由5颗静止轨道卫星(同步卫星)和30颗非静止轨道卫星组成,30颗非静止轨道卫星中有27颗是中轨道卫星,中轨道卫星的高度约为21500km,同步卫星的高度约为36000km,与中轨道卫星相比,同步卫星的( )| A. | 线速度较大 | B. | 角速度较大 | C. | 周期较大 | D. | 向心加速度较大 |
分析 卫星绕地球做圆周运动,万有引力提供向心力,由牛顿第二定律求出卫星的线速度、角速度、周期与向心加速度,然后比较其大小.
解答 解:卫星绕地球做匀速圆周运动,万有引力提供向心力;
A、由牛顿第二定律得:G$\frac{Mm}{{r}^{2}}$=m$\frac{{v}^{2}}{r}$,解得:v=$\sqrt{\frac{GM}{r}}$,由题意可知,同步卫星的轨道半径大于中轨道卫星的半径,即:r同步>r中轨道,则同步卫星的线速度较小,故A错误;
B、由牛顿第二定律得:G$\frac{Mm}{{r}^{2}}$=mω2r,解得:ω=$\sqrt{\frac{GM}{{r}^{3}}}$,由题意可知,同步卫星的轨道半径大于中轨道卫星的半径,即:r同步>r中轨道,则同步卫星的角速度小于中轨道卫星的角速度,故B错误;
C、由牛顿第二定律得:G$\frac{Mm}{{r}^{2}}$=m$(\frac{2π}{T})^{2}$r,解得:T=2π$\sqrt{\frac{{r}^{3}}{GM}}$,由题意可知,同步卫星的轨道半径大于中轨道卫星的半径,即:r同步>r中轨道,则同步卫星的周期大于中轨道卫星的周期,故C正确;
D、由牛顿第二定律得:G$\frac{Mm}{{r}^{2}}$=ma,解得:a=$\frac{GM}{{r}^{2}}$由题意可知,同步卫星的轨道半径大于中轨道卫星的半径,即:r同步>r中轨道,则同步卫星的向心加速度小于中轨道卫星的向心加速度,故D错误;
故选:C.
点评 本题考查了万有引力定律的应用,知道万有引力提供向心力,应用万有引力定律与牛顿第二定律即可解题,要掌握万有引力定律应用的基本原理.

练习册系列答案
相关题目
19. 如图所示,质量为m的物体A在竖直向上的力F(F<mg)作用下静止于斜面上.若减小力F,则( )
如图所示,质量为m的物体A在竖直向上的力F(F<mg)作用下静止于斜面上.若减小力F,则( )
 如图所示,质量为m的物体A在竖直向上的力F(F<mg)作用下静止于斜面上.若减小力F,则( )
如图所示,质量为m的物体A在竖直向上的力F(F<mg)作用下静止于斜面上.若减小力F,则( )| A. | 物体A所受合力不变 | B. | 斜面对物体A的支持力不变 | ||
| C. | 斜面对物体A的摩擦力不变 | D. | 斜面对物体A的摩擦力可能为零 |
20.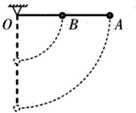 如图所示,一长为L的轻质细杆可绕其一端O点在竖直平面内自由转动,在杆的中点和另一端分别固定两个质量相等的可看作质点的A、B小球.重力加速度为g,不计空气阻力.现将杆从水平位置静止释放,下列说法正确的是( )
如图所示,一长为L的轻质细杆可绕其一端O点在竖直平面内自由转动,在杆的中点和另一端分别固定两个质量相等的可看作质点的A、B小球.重力加速度为g,不计空气阻力.现将杆从水平位置静止释放,下列说法正确的是( )
 如图所示,一长为L的轻质细杆可绕其一端O点在竖直平面内自由转动,在杆的中点和另一端分别固定两个质量相等的可看作质点的A、B小球.重力加速度为g,不计空气阻力.现将杆从水平位置静止释放,下列说法正确的是( )
如图所示,一长为L的轻质细杆可绕其一端O点在竖直平面内自由转动,在杆的中点和另一端分别固定两个质量相等的可看作质点的A、B小球.重力加速度为g,不计空气阻力.现将杆从水平位置静止释放,下列说法正确的是( )| A. | A球机械能守恒 | |
| B. | A球运动到最低点时,重力的功率为零 | |
| C. | A球到达最低点时的速度为2$\sqrt{\frac{3gL}{5}}$ | |
| D. | 以后A球一定能回到释放点 |
17. 如图所示,两物体A、B质量相等,相互接触放在光滑水平面上,对物体A施以水平向右推力F1,同时对B施加水平向左推力F2,且F1>F2,则物体B对物体A的作用力大小是( )
如图所示,两物体A、B质量相等,相互接触放在光滑水平面上,对物体A施以水平向右推力F1,同时对B施加水平向左推力F2,且F1>F2,则物体B对物体A的作用力大小是( )
 如图所示,两物体A、B质量相等,相互接触放在光滑水平面上,对物体A施以水平向右推力F1,同时对B施加水平向左推力F2,且F1>F2,则物体B对物体A的作用力大小是( )
如图所示,两物体A、B质量相等,相互接触放在光滑水平面上,对物体A施以水平向右推力F1,同时对B施加水平向左推力F2,且F1>F2,则物体B对物体A的作用力大小是( )| A. | $\frac{{F}_{1}-{F}_{2}}{2}$ | B. | $\frac{{F}_{1}+{F}_{2}}{2}$ | C. | $\frac{{F}_{1}}{2}$ | D. | $\frac{{F}_{2}}{2}$ |
14. 如图所示,A、B是匀强电场中相距4cm的两点,其连线与电场方向的夹角为60°,两点间的电势差为20V,则电场强度大小为( )
如图所示,A、B是匀强电场中相距4cm的两点,其连线与电场方向的夹角为60°,两点间的电势差为20V,则电场强度大小为( )
 如图所示,A、B是匀强电场中相距4cm的两点,其连线与电场方向的夹角为60°,两点间的电势差为20V,则电场强度大小为( )
如图所示,A、B是匀强电场中相距4cm的两点,其连线与电场方向的夹角为60°,两点间的电势差为20V,则电场强度大小为( )| A. | 5V/m | B. | 50V/m | C. | 1×102V/m | D. | 1×103V/m |
18. 如图所示,内壁光滑的锥形漏斗固定不动,其轴线垂直于水平面,两个质量相同的小球A和B紧贴着漏斗内壁分别在图中所示的水平面内做匀速圆周运动,则( )
如图所示,内壁光滑的锥形漏斗固定不动,其轴线垂直于水平面,两个质量相同的小球A和B紧贴着漏斗内壁分别在图中所示的水平面内做匀速圆周运动,则( )
 如图所示,内壁光滑的锥形漏斗固定不动,其轴线垂直于水平面,两个质量相同的小球A和B紧贴着漏斗内壁分别在图中所示的水平面内做匀速圆周运动,则( )
如图所示,内壁光滑的锥形漏斗固定不动,其轴线垂直于水平面,两个质量相同的小球A和B紧贴着漏斗内壁分别在图中所示的水平面内做匀速圆周运动,则( )| A. | 球A的角速度等于球B的角速度 | |
| B. | 球A的线速度等于球B的线速度 | |
| C. | 球A的向心加速度等于球B的向心加速度 | |
| D. | 球A对内壁的压力大于球B对内壁的压力 |
19.关于第一宇宙速度的说法中正确的是( )
| A. | 第一宇宙速度是发射卫星的最大速度 | |
| B. | 第一宇宙速度的数值是11.2km/s | |
| C. | 第一宇宙速度是近地绕地卫星应具有的速度 | |
| D. | 第一宇宙速度是卫星做圆周运动的最小线速度 |
 在“探究加速度与力、质量的关系”实验中,采用如图1所示的实验装置,小车及车载砝码的质量用M表示,盘及盘中砝码的质量用m表示.
在“探究加速度与力、质量的关系”实验中,采用如图1所示的实验装置,小车及车载砝码的质量用M表示,盘及盘中砝码的质量用m表示.