题目内容
11. 如图所示为一个水平放置的平行板电容器,两板电压U=2V,两板距离d=10cm,两板间有磁感应强度B1=2T的匀强磁场,方向垂直纸面向里,一带正电的粒子(不计重力)比荷为$\frac{q}{m}$=25c/kg,从左边射入,恰好沿水平直线AC运动,从右边射出并垂直MN进入以MN、PQ两竖直线为边界的匀强电场,已知电场强度E=20N/C,方向竖直向下,MN、PQ的距离为L=20cm.在PQ的右边有垂直纸面向里的匀强磁场B2=4T,KG是平行PQ的挡板,KG与PQ的距离S=20cm,粒子打在挡板上后被吸收.
如图所示为一个水平放置的平行板电容器,两板电压U=2V,两板距离d=10cm,两板间有磁感应强度B1=2T的匀强磁场,方向垂直纸面向里,一带正电的粒子(不计重力)比荷为$\frac{q}{m}$=25c/kg,从左边射入,恰好沿水平直线AC运动,从右边射出并垂直MN进入以MN、PQ两竖直线为边界的匀强电场,已知电场强度E=20N/C,方向竖直向下,MN、PQ的距离为L=20cm.在PQ的右边有垂直纸面向里的匀强磁场B2=4T,KG是平行PQ的挡板,KG与PQ的距离S=20cm,粒子打在挡板上后被吸收.(1)试问电容器的上下板哪板电势高?求粒子离开MN时的速度大小.
(2)求粒子进入B2后在B2中运动的时间.
(3)为使粒子打不到档板KG上,档板与PQ的距离至少为多少?
分析 (1)带正电的粒子在平行板电容器间做匀速直线运动,电场力与洛仑兹力平衡,根据左手定则,洛仑兹力向上,根据平衡条件,电场力向下,故可以确定上面的极板带正电荷;
(2)进入电场后,做类似平抛运动,根据分运动公式列式求解末速度大小和方向;在磁场中,洛仑兹力提供向心力,根据牛顿第二定律列式求解轨道半径,画出运动轨迹,得到运动时间;
(3)考虑临界情况,粒子轨迹与KG相切,结合几何关系列式分析即可.
解答 解:(1)粒子做匀速直线运动,电场力向下,故上板带正电荷,电势高;
粒子沿AC匀速运动,洛伦兹力等于电场力,有:B1qv1=qE1,
其中:${E_1}=\frac{U}{d}$,
代入数据得:v1=10m/s;
(2)粒子在电场中类平抛,有:l=v1t1,
${v_F}=a{t_1}=\frac{qE}{m}{t_1}$,
得:vy=10m/s,
进入B2的速度为:${v_2}=\sqrt{v_1^2+v_y^2}=10\sqrt{2}m/s$,
与PQ的夹角为:$θ=\frac{π}{4}$,
在磁场中运动,洛伦兹力提供向心力,有:${B_2}q{v_2}=m\frac{v_2^2}{r}$,
代入数据解得半径为:$r=\frac{{\sqrt{2}}}{10}m$, 轨迹如图,圆心角α=$\frac{π}{2}$,
轨迹如图,圆心角α=$\frac{π}{2}$,
运动时间为:${t_2}=\frac{πr}{{2{v_2}}}=\frac{π}{200}s=1.57×{10^{-2}}s$;
(3)当KG与粒子在磁场中运动轨迹恰好相切时:
$S'=r+rsin\frac{π}{4}=\frac{{\sqrt{2}+1}}{10}m=0.2414m=24.14m$,
即KG与PQ的最小距离为24.14m;
答:(1)电容器的上板电势高,粒子离开MN时的速度大小为10m/s.
(2)粒子进入B2后在B2中运动的时间为1.57×10-2s.
(3)为使粒子打不到档板KG上,档板与PQ的距离至少为24.14m.
点评 本题关键是明确粒子的受力情况和运动情况,分匀速直线运动、类似平抛运动和匀速圆周运动进行分析,画出轨迹,结合几何关系分析,不难.

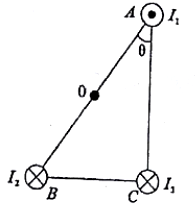 三根平行的长直通电导线,分别通过一个直角三角形的三个顶点且与三角形所在平面垂直,如图所示,θ=30°,O为斜边的中点,已知直线电流在某点产生的磁场,其磁感应强度B的大小与电流强度成正比,与点到通电导线的距离r成反比,已知I3=2I1=2I2,I1在O点产生的磁场感应强度大小为B,则关于O点的磁感应强度,下列说法正确的是( )
三根平行的长直通电导线,分别通过一个直角三角形的三个顶点且与三角形所在平面垂直,如图所示,θ=30°,O为斜边的中点,已知直线电流在某点产生的磁场,其磁感应强度B的大小与电流强度成正比,与点到通电导线的距离r成反比,已知I3=2I1=2I2,I1在O点产生的磁场感应强度大小为B,则关于O点的磁感应强度,下列说法正确的是( )| A. | 2B,沿OC方向 | B. | 2B,垂直AC向右 | C. | 2$\sqrt{3}$B,垂直AC向右 | D. | 0 |
| A. | $\frac{3π{G}_{2}}{G({G}_{2}-{G}_{1}){T}^{2}}$ | B. | $\frac{3π({G}_{2}-{G}_{1})}{GG{{\;}_{2}T}^{2}}$ | ||
| C. | $\frac{3π{G}_{2}}{GG{{\;}_{1}T}^{2}}$ | D. | $\frac{3π{G}_{1}}{G{G}_{2}{T}^{2}}$ |
 如图所示,在区域Ⅰ和区域Ⅱ内分别存在与纸面垂直的匀强磁场,MN为两区域的分界线,一带电粒子沿着弧线apd由区域Ⅰ运动到区域Ⅱ.已知ap段的弧长大于pb段的弧长,带电粒子仅受到磁场力的作用.下列说法正确的是( )
如图所示,在区域Ⅰ和区域Ⅱ内分别存在与纸面垂直的匀强磁场,MN为两区域的分界线,一带电粒子沿着弧线apd由区域Ⅰ运动到区域Ⅱ.已知ap段的弧长大于pb段的弧长,带电粒子仅受到磁场力的作用.下列说法正确的是( )| A. | 区域Ⅰ和区域Ⅱ的磁感应强度方向相反 | |
| B. | 粒子在区域Ⅱ中的速率小于在区域Ⅰ中的速率 | |
| C. | 区域Ⅰ的磁感应强速小于Ⅱ的磁感应强度 | |
| D. | 粒子在ap段的运动时间大于在pb段的运动时间 |
 如图初速为零的电子经加速电场加速后,垂直射入偏转电场,射出时偏转位移为d,若要使d增大些,下列哪些措施是可行的( )
如图初速为零的电子经加速电场加速后,垂直射入偏转电场,射出时偏转位移为d,若要使d增大些,下列哪些措施是可行的( )| A. | 增大偏转电场极板间距离 | B. | 增大加速电压U0 | ||
| C. | 增大偏转电压U | D. | 增大偏转电场的极板长度 |
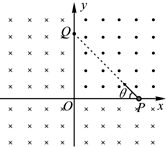 如图所示,在xoy平面直角坐标系中,直线PQ与y轴成θ=45°角,且OP=L,第一象限分布着垂直纸面向外的匀强磁场,另外三个象限分布着垂直纸面向里的匀强磁场,磁感应强度大小都为B,现有一质量为m、电荷量为q的带负电微粒从P点沿PQ方向射出,不计微粒的重力.求:
如图所示,在xoy平面直角坐标系中,直线PQ与y轴成θ=45°角,且OP=L,第一象限分布着垂直纸面向外的匀强磁场,另外三个象限分布着垂直纸面向里的匀强磁场,磁感应强度大小都为B,现有一质量为m、电荷量为q的带负电微粒从P点沿PQ方向射出,不计微粒的重力.求: 如图所示,相距为d的平行金属板M、N间存在匀强电场和垂直纸面向里、磁感应强度为B0的匀强磁场;在xOy直角坐标系平面内,第一象限有沿y轴负方向场强为E的匀强电场,第四象限有垂直坐标轴向外的半圆形匀强磁场ODC.一质量为m、带电量为q的正离子(不计重力)以初速度v0沿平行于金属板方向射入两板间并做匀速直线运动,从P点垂直y轴进入第一象限,经过x轴上的A点射出电场磁场.已知离子过A点时的速度方向与x轴成45°角,且A为半圆形磁场的圆心.求:
如图所示,相距为d的平行金属板M、N间存在匀强电场和垂直纸面向里、磁感应强度为B0的匀强磁场;在xOy直角坐标系平面内,第一象限有沿y轴负方向场强为E的匀强电场,第四象限有垂直坐标轴向外的半圆形匀强磁场ODC.一质量为m、带电量为q的正离子(不计重力)以初速度v0沿平行于金属板方向射入两板间并做匀速直线运动,从P点垂直y轴进入第一象限,经过x轴上的A点射出电场磁场.已知离子过A点时的速度方向与x轴成45°角,且A为半圆形磁场的圆心.求: 如图所示,水平地面上方分布着水平向右的匀强电场,有-$\frac{1}{4}$圆弧形的绝缘硬质管竖直固定在匀强电场中.圆心与管口在同一水平线上,管的半径为R,下端管口切线水平,离水平地面的距离为h,有一质量为m的带正电(+q)小球从管的上端口A由静止释放,小球与管间摩擦不计,小球从下端管口飞出时,对管壁压力为4mg,求:
如图所示,水平地面上方分布着水平向右的匀强电场,有-$\frac{1}{4}$圆弧形的绝缘硬质管竖直固定在匀强电场中.圆心与管口在同一水平线上,管的半径为R,下端管口切线水平,离水平地面的距离为h,有一质量为m的带正电(+q)小球从管的上端口A由静止释放,小球与管间摩擦不计,小球从下端管口飞出时,对管壁压力为4mg,求: