设A是△ABC中的最小角，且cosA=

a-1

a+1

，则实数a的取值范围是（　　）

函数y=

-cosx

+

sinx

的定义域是（　　）

已知函数y=2cosx的定义域为[

π

3

，π]，值域为[a，b]，则b-a的值是（　　）

已知函数f（x）=ax²+bcosx，g（x）=csinx，且abc≠0，若f（2）+g（2）=3，f（-2）+g（-2）=1，则f（2）=（　　）

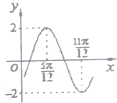函数f（x）=2sin（ωx+φ）（ω＞0，-

π

2

＜φ＜

π

2

）的部分图象如图所示，f（x）的图象左移

π

4

个单位得到的g（x）的图象，则g（x）的一条对称轴可以是（　　）

已知函数f(x)=2sin(2x+

π

6

)-1(x∈R)则f（x）在区间[0，

π

2

]上的最大值与最小值分别是（　　）

对于函数f（x），若存在区间A=[m，n]，使得{y|y=f（x），x∈A}=A，则称函数f（x）为“可等域函数”，区间A为函数f（x）的一个“可等域区间”．给出下列4个函数：
①f（x）=sin（

π

2

x）；
②f（x）=2x²-1；
③f（x）=|1-2^x|；      
④f（x）=log₂（2x-2）．
其中存在唯一“可等域区间”的“可等域函数”为（　　）

设函数f（x）=|cosx|+|sinx|，下列四个结论正确的是（　　）
①f（x）是奇函数；                        
②f（x）关于直线x=

3π

4

对称；
③当x∈[0，2π]时，f（x）∈[1，

2

]；         
④当x∈[0，

π

2

]时，f（x）单调递增．

已知f（x）=sin（ωx+φ）（ω＞0，|φ|＜

π

2

），满足f（x）=-f（x+π），f（0）=

1

2

，则g（x）=2cos（ωx+φ）在区间[0，

π

2

]上的最大值与最小值之和为（　　）