Question

设函数f（x）=|cosx|+|sinx|，下列四个结论正确的是（　　）
①f（x）是奇函数；                        
②f（x）关于直线x=

3π

4

对称；
③当x∈[0，2π]时，f（x）∈[1，

2

]；         
④当x∈[0，

π

2

]时，f（x）单调递增．

• A、①③
• B、②④
• C、③④
• D、②③

Answer 1

分析：分别根据函数的奇偶性，对称性和单调性的性质即可得到结论．

解答：解：①f（-x）=|cos（-x）|+|sin（-x）|=|cosx|+|sinx|=f（x），
∴f（x）是偶函数；∴①错误．
②∵f（x+

3π

4

）=|sin（x+

3π

4

）|+|cos（x+

3π

4

）|=|

2

2

（cosx-sinx）|+|

2

2

（cosx+sinx）|，
f（

3π

4

-x）=|sin（

3π

4

-x）|+|cos（

3π

4

-x）|=|

2

2

（cosx-sinx）|+|

2

2

（cosx+sinx）|，
∴f（x+

3π

4

）=f（

3π

4

-x），∴函数f（x）关于直线x=

3π

4

对称；∴②正确．
③f（x）=

sin?x+cos?x，0≤x≤ π 2 sin?x-cos?x， π 2 ＜x≤π -sin?x-cos?x，π＜x≤ 3π 2 cos?x-sin?x， 3π 2 ＜x≤2π

，
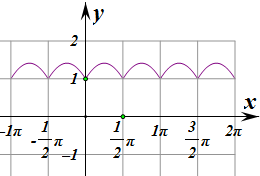
作出函数f（x）的图象可知：当x∈[0，2π]时，f（x）∈[1，

2

]； 
∴③正确．
④当x∈[0，

π

2

]时，由图象可知f（x）不单调．
∴④错误．
故选：D．

点评：本题主要考查三角函数的图象和性质，利用条件求出函数的表达式是解决本题的关键．