题目内容
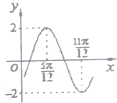 函数f(x)=2sin(ωx+φ)(ω>0,-
函数f(x)=2sin(ωx+φ)(ω>0,-| π |
| 2 |
| π |
| 2 |
| π |
| 4 |
| A、x=0 | ||
B、x=
| ||
C、x=
| ||
D、x=-
|
分析:根据函数的图象求出函数f(x)的表达式,进而求出g(x)的表达式,即可得到结论.
解答:解:由图象可知
=
-
=
,即函数的周期T=π,∴ω=2,
∵f(
)=2sin(2×
+φ)=2sin(
+φ)=2,
即sin(
+φ)=1
∴
+φ=
+kπ,k∈Z,
即φ=-
+kπ,k∈Z,
∵-
<φ<
,
∴φ=-
,即f(x)=2sin(2x-
),
将f(x)的图象左移
个单位得到的g(x)的图象,
则g(x)=f(x+
)=2sin(2x+
-
)=2cos(2x-
),
由2x-
=kπ,k∈Z,
解得x=
+
,
∴当k=-1时,x=-
,
故选:D.
| T |
| 2 |
| 11π |
| 12 |
| 5π |
| 12 |
| π |
| 2 |
∵f(
| 5π |
| 12 |
| 5π |
| 12 |
| 5π |
| 6 |
即sin(
| 5π |
| 6 |
∴
| 5π |
| 6 |
| π |
| 2 |
即φ=-
| π |
| 3 |
∵-
| π |
| 2 |
| π |
| 2 |
∴φ=-
| π |
| 3 |
| π |
| 3 |
将f(x)的图象左移
| π |
| 4 |
则g(x)=f(x+
| π |
| 4 |
| π |
| 2 |
| π |
| 3 |
| π |
| 3 |
由2x-
| π |
| 3 |
解得x=
| π |
| 6 |
| kπ |
| 2 |
∴当k=-1时,x=-
| π |
| 3 |
故选:D.
点评:本题主要考查三角函数的图象和性质,利用图象求出函数的解析式是解决本题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 (2013•盐城三模)已知函数f (x)=2sin(ωx+?)(ω>0)的部分图象如图所示,则ω=
(2013•盐城三模)已知函数f (x)=2sin(ωx+?)(ω>0)的部分图象如图所示,则ω=