函数f(x)=
ax3+
ax2-2ax+2a+1的图象经过四个象限，则实数a的取值范围是（ ）
| 1 |
| 3 |
| 1 |
| 2 |
A、a＞-
| ||||
B、-
| ||||
C、a＞-
| ||||
D、-
|
已知双曲线an-1y2-anx2=an-1an的焦点在y轴上，一条渐近线方程为y=
x，其中{an}是以4为首项的正数数列，则数列{an}的通项公式是（ ）
| 2 |
A、an=2
| ||
| B、an=21-n | ||
| C、an=4n-2 | ||
| D、an=2n+1 |
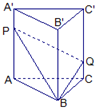如图直三棱柱ABC-A1B1C1的体积为V，点P、Q分别在侧棱AA1和CC1上，AP=C1Q，则四棱锥B-APQC的体积为（ ）A、
| ||
B、
| ||
C、
| ||
D、
|
给定四条曲线：①x2+y2=
，②
+
=1，③x2+
=1，④
+y2=1，其中与直线x+y-
=0仅有一个交点的曲线是（ ）
| 5 |
| 2 |
| x2 |
| 9 |
| y2 |
| 4 |
| y2 |
| 4 |
| x2 |
| 4 |
| 5 |
| A、①②③ | B、②③④ |
| C、①②④ | D、①③④ |
已知实数a满足1＜a＜2．命题P：函数y=loga（2-ax）在区间[0，1]上是减函数，命题Q：|x|＜1是x＜a的充分不必要条件，则（ ）
| A、“P或Q”为真命题 | B、“P且Q”为假命题 | C、“┐P且Q”为真命题 | D、“┐P或┐Q”为真命题 |
在等差数列{an}中，a1，a2，a5成等比数列，且a1+a2+a5=13，则数列{an}的公差为（ ）
| A、2 | ||
| B、0 | ||
| C、2或0 | ||
D、
|
将函数y=sin(x-
)的图象先向左平移
，然后将所得图象上所有点的横坐标变为原来的
（纵坐标不变），则所得到的图象对应的函数解析式为（ ）
| π |
| 3 |
| π |
| 6 |
| 1 |
| 2 |
| A、y=-cos2x | ||
| B、y=sin2x | ||
C、y=sin(2x-
| ||
| D、y=sin4x |
复数z=（a+i）（3-4i）∈R，则实数a的值为（ ）
A、-
| ||
B、
| ||
C、
| ||
D、-
|