【题目】在中， 分别是角的对边，已知，现有以下判断：

①不可能等于15； ②；

③作关于的对称点的最大值是；

④若为定点，则动点的轨迹围成的封闭图形的面积是。请将所有正确的判断序号填在横线上______________。

在直角坐标系中，以为极点， 轴的正半轴为极轴建立极坐标系，曲线的方程是，将向上平移2个单位得到曲线．　

（1）求曲线的极坐标方程；

（2）直线的参数方程为（为参数），判断直线与曲线的位置关系．

【题目】已知函数．

（1）试讨论的单调性；

（2）若有两个极值点， ，且，求证： ．

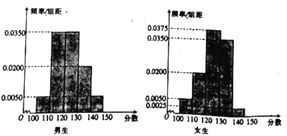
（1）从样本中分数小于110分的学生中随机抽取两人，求两人性别相同的概率；

（2）若规定分数不小于130分的学生为“数学尖子生”，试判断能否在犯错误的概率不超过0.1的前提下认为“数学尖子生与性别有关”．

附：

【题目】已知角始边与轴的非负半轴重合，与圆相交于点，终边与圆相交于点，点在轴上的射影为， 的面积为，函数的图象大致是（ ）

A. B.

C. D.

【题目】已知函数，.

（1）设函数，试讨论函数零点的个数；

（2）若，，求证：

（Ⅰ）如果共享单车用户人数超过5百万的城市称为“优质潜力城市”，否则“非优”，请据此判断是否有85%的把握认为“优质潜力城市”与共享单车品牌有关？

（Ⅱ）如果不考虑其它因素，为拓展市场，甲品牌要从这5个城市中选出3个城市进行大规模宣传．

①在城市Ⅰ被选中的条件下，求城市Ⅱ也被选中的概率；

②以表示选中的城市中用户人数超过5百万的个数，求随机变量的分布列及数学期望．

下面临界值表供参考：

参考公式： K2＝，n＝a＋b＋c＋d

【题目】如图，在Rt中， ，点、分别在线段、上，且，将沿折起到的位置，使得二面角的大小为.

（1）求证：；

（2）当点为线段的靠近点的三等分点时，求与平面 所成角的正弦值.

【题目】对于函数，下列说法正确的有（ ）

①在处取得极大值；②有两个不同的零点；

③；④若在上恒成立，则.

A. 4个 B. 3个 C. 2个 D. 1个

【题目】已知函数

（1）当时，求的极值；

（2）若有两个不同的极值点 ，求的取值范围;