题目内容
【题目】某学校高三年级有学生750人,其中男生450人,女生300人,为了研究学生的数学成绩是否与性别有关,现采用分层抽样的方法,从中抽取了100名学生,先统计了他们期中考试的数学分数,然后按性别分别分为男、女两组,再将两组学生的分数分成5组,分别加以统计,得到如图所示的频率分布直方图.
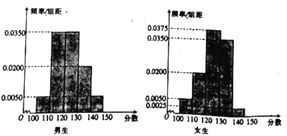
(1)从样本中分数小于110分的学生中随机抽取两人,求两人性别相同的概率;
(2)若规定分数不小于130分的学生为“数学尖子生”,试判断能否在犯错误的概率不超过0.1的前提下认为“数学尖子生与性别有关”.
附: 
| 0.100 | 0.050 | 0.010 | 0.001 |
| 2.706 | 3.841 | 6.635 | 10.828 |
【答案】(1)![]() ;(2)不能在犯错误的概率不超过0.1的前提下认为“数学尖子生与性别有关”.
;(2)不能在犯错误的概率不超过0.1的前提下认为“数学尖子生与性别有关”.
【解析】试题分析:(1)由频率分布直方图知分数小于等于110分的学生中,男生有![]() (人),记为
(人),记为![]() ,
, ![]() ,
, ![]() ;女生有
;女生有![]() (人),记为
(人),记为![]() ,
, ![]() .从中随机抽取2名学生,基本事件为10个,其中,两名学生性别相同的基本事件有4个即可求概率p(2) 由频率分布直方图可知,在抽取的100名学生中,男生数学尖子生有
.从中随机抽取2名学生,基本事件为10个,其中,两名学生性别相同的基本事件有4个即可求概率p(2) 由频率分布直方图可知,在抽取的100名学生中,男生数学尖子生有![]() (人),女生数学尖子生有
(人),女生数学尖子生有![]() (人),画出列联表,计算
(人),画出列联表,计算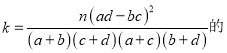 值,即可下结论.
值,即可下结论.
试题解析:
(1)由已知得,抽取的100名学生中,男生60名,女生40名,其中分数小于等于110分的学生中,男生有![]() (人),记为
(人),记为![]() ,
, ![]() ,
, ![]() ;女生有
;女生有![]() (人),记为
(人),记为![]() ,
, ![]() .从中随机抽取2名学生,基本事件为
.从中随机抽取2名学生,基本事件为![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 共10个,其中,两名学生性别相同的基本事件有4个:
共10个,其中,两名学生性别相同的基本事件有4个: ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
故所求的概率![]() .
.
(2)由频率分布直方图可知,在抽取的100名学生中,男生数学尖子生有![]() (人),女生数学尖子生有
(人),女生数学尖子生有![]() (人),
(人),
据此可得![]() 列联表如下:
列联表如下:
数学尖子生 | 非数学尖子生 | 合计 | |
男生 | 15 | 45 | 60 |
女生 | 15 | 25 | 40 |
合计 | 30 | 70 | 100 |
所以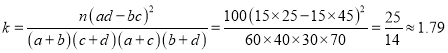 ,
,
∵![]() ,∴不能在犯错误的概率不超过0.1的前提下认为“数学尖子生与性别有关”.
,∴不能在犯错误的概率不超过0.1的前提下认为“数学尖子生与性别有关”.

 名校课堂系列答案
名校课堂系列答案