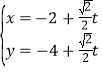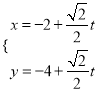题目内容
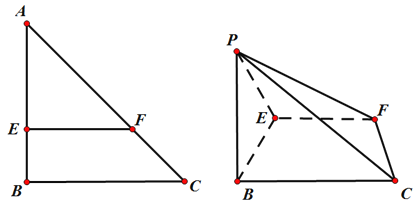
【题目】如图,在Rt![]() 中,
中,![]() ,点
,点![]() 、
、![]() 分别在线段
分别在线段![]() 、
、![]() 上,且
上,且![]() ,将
,将![]() 沿
沿![]() 折起到
折起到![]() 的位置,使得二面角
的位置,使得二面角![]() 的大小为
的大小为![]() .
.
(1)求证:![]() ;
;
(2)当点![]() 为线段
为线段![]() 的靠近
的靠近![]() 点的三等分点时,求
点的三等分点时,求![]() 与平面
与平面![]() 所成角
所成角![]() 的正弦值.
的正弦值.
【答案】(1)见解析(2)![]()
【解析】试题分析:(1)由等腰三角形的性质可得![]() ,
,![]() ,翻折后垂直关系没变,仍有
,翻折后垂直关系没变,仍有![]() ,
,![]() 平面
平面![]() ,从而得
,从而得![]() ; (2)
; (2) ![]() 二面角
二面角![]() 的平面角,由余弦定理得
的平面角,由余弦定理得![]() ,由勾股定理可得
,由勾股定理可得![]() ,
,![]() 两两垂直,以
两两垂直,以![]() 为原点,
为原点,![]() 所在直线为
所在直线为![]() 轴,
轴,![]() 所在直线为
所在直线为![]() 轴,建立空间直角坐标系,求出平面
轴,建立空间直角坐标系,求出平面![]() 的法向量与
的法向量与![]() 的方向向量,利用空间向量夹角余弦公式可得结果.
的方向向量,利用空间向量夹角余弦公式可得结果.
试题解析:(1)![]()
![]()
![]()
![]()
![]()
![]() ,翻折后垂直关系没变,仍有
,翻折后垂直关系没变,仍有![]() ,
,![]()
![]()
![]() .
.
(2) ![]()
![]() ,
,![]()
![]() 二面角
二面角![]() 的平面角,
的平面角,
![]() ,又
,又![]() ,由余弦定理得
,由余弦定理得![]() ,
,
![]() ,
,![]() ,
,![]() 两两垂直.
两两垂直.
以![]() 为原点,
为原点,![]() 所在直线为
所在直线为![]() 轴,
轴,![]() 所在直线为
所在直线为![]() 轴,建立如图直角坐标系.
轴,建立如图直角坐标系.
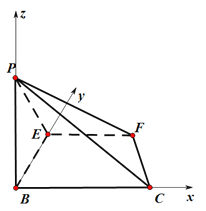
则![]()
![]()
![]()
![]()
![]()
设平面![]() 的法向量
的法向量![]()
由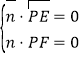 可得
可得![]()
![]()
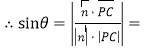
![]() .
.
故PC与平面PEF所成的角的正弦值为 ![]() .
.
【方法点晴】本题主要考查利用空间向量求线面角,属于难题.空间向量解答立体几何问题的一般步骤是:(1)观察图形,建立恰当的空间直角坐标系;(2)写出相应点的坐标,求出相应直线的方向向量;(3)设出相应平面的法向量,利用两直线垂直数量积为零列出方程组求出法向量;(4)将空间位置关系转化为向量关系;(5)根据定理结论求出相应的角和距离.

 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案【题目】某学校运动会的立定跳远和30秒跳绳两个单项比赛分成预赛和决赛两个阶段.下表为10名学生的预赛成绩,其中有三个数据模糊.
学生序号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
立定跳远(单位:米) | 1.96 | 1.92 | 1.82 | 1.80 | 1.78 | 1.76 | 1.74 | 1.72 | 1.68 | 1.60 |
30秒跳绳(单位:次) | 63 | a | 75 | 60 | 63 | 72 | 70 | a1 | b | 65 |
在这10名学生中,进入立定跳远决赛的有8人,同时进入立定跳远决赛和30秒跳绳决赛的有6人,则
(A)2号学生进入30秒跳绳决赛
(B)5号学生进入30秒跳绳决赛
(C)8号学生进入30秒跳绳决赛
(D)9号学生进入30秒跳绳决赛