9.若a>b>1,0<c<1,则( )
| A. | ac<bc | B. | abc<bac | C. | logac<logbc | D. | alogbc<blogac |
8.已知双曲线C:$\frac{x^2}{a^2}-\frac{y^2}{b^2}$=1(a>0,b>0)的一条渐近线方程为y=$\frac{{\sqrt{5}}}{2}$x,且与椭圆$\frac{x^2}{12}+\frac{y^2}{3}$=1有公共焦点,则C的方程为( )
| A. | $\frac{x^2}{8}-\frac{y^2}{10}=1$ | B. | $\frac{x^2}{5}-\frac{y^2}{4}=1$ | C. | $\frac{x^2}{4}-\frac{y^2}{5}=1$ | D. | $\frac{x^2}{4}-\frac{y^2}{3}=1$ |
7.设有下面四个命题
p1:若复数z满足$\frac{1}{z}$∈R,则z∈R;
p2:若复数z满足z2∈R,则z∈R;
p3:若复数z1,z2满足z1z2∈R,则z1=$\overline{z_2}$;
p4:若复数z∈R,则$\overline{z}$∈R.
其中的真命题为( )
p1:若复数z满足$\frac{1}{z}$∈R,则z∈R;
p2:若复数z满足z2∈R,则z∈R;
p3:若复数z1,z2满足z1z2∈R,则z1=$\overline{z_2}$;
p4:若复数z∈R,则$\overline{z}$∈R.
其中的真命题为( )
| A. | p2,p3 | B. | p2,p4 | C. | p1,p3 | D. | p1,p4 |
6.已知向量$\overrightarrow{BA}=(\frac{1}{2},\frac{{\sqrt{3}}}{2})$,$\overrightarrow{BC}=(\frac{{\sqrt{3}}}{2},\frac{1}{2})$,则∠ABC=( )
| A. | 120° | B. | 45° | C. | 30° | D. | 60° |
5.设集合A={1,2,4},B={x|x2-4x+m=0}.若A∩B={1},则B=( )
| A. | {1,-3} | B. | {1,5} | C. | {1,0} | D. | {1,3} |
4.在R上定义运算$|\begin{array}{l}{a}&{c}\\{b}&{d}\end{array}|$=ad-bc,若f(x)=$|\begin{array}{l}{2sinx}&{2sinx}\\{\sqrt{3}sinx}&{cosx}\end{array}|$,x∈[0,π],则f(x)的递增区间为( )
| A. | [0,$\frac{π}{6}$],[$\frac{2π}{3}$,π] | B. | [$\frac{π}{6}$,$\frac{2π}{3}$] | C. | [0,$\frac{π}{12}$],[$\frac{7π}{12}$,π] | D. | [$\frac{π}{12}$,$\frac{7π}{12}$] |
1.已知集合M={ x|x≥-$\frac{1}{2}$},N={x|1-x2≥0},则M∪N=( )
| A. | [-$\frac{1}{2}$,1] | B. | [-1,1] | C. | (-1,+∞) | D. | [-1,+∞) |
20.已知命题p:?x∈R,sinx>1,命题q:?a,b∈(0,+∞),$\frac{a+b}{2}$≥$\sqrt{ab}$,则下列判断错误的是( )
0 240848 240856 240862 240866 240872 240874 240878 240884 240886 240892 240898 240902 240904 240908 240914 240916 240922 240926 240928 240932 240934 240938 240940 240942 240943 240944 240946 240947 240948 240950 240952 240956 240958 240962 240964 240968 240974 240976 240982 240986 240988 240992 240998 241004 241006 241012 241016 241018 241024 241028 241034 241042 266669
| A. | p或q为真,非q为假 | B. | p或q为真,非p为真 | ||
| C. | p且q为假,非p为假 | D. | p且q为假,p或q为真 |
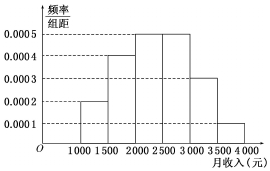 某市统计局就本地居民的月收入调查了10000人,并根据所得数据画了样本的频率分布直方图(每个分组包括左端点,不包括右端点,如第一组表示月收入在[1000,1500)(单位:元)).
某市统计局就本地居民的月收入调查了10000人,并根据所得数据画了样本的频率分布直方图(每个分组包括左端点,不包括右端点,如第一组表示月收入在[1000,1500)(单位:元)).