8.设a,b,c都是正实数,且a+b+c=1,则$({\frac{1}{a}-1})({\frac{1}{b}-1})({\frac{1}{c}-1})$的取值范围是( )
| A. | [0,$\frac{1}{8}$) | B. | [8,+∞) | C. | [1,8) | D. | [$\frac{1}{8}$,1) |
7.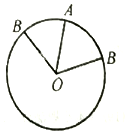 如图,点A为周长为3的圆周上的一定点,若在该圆周上随机取一点B,则劣弧AB的长度小于1的概率为( )
如图,点A为周长为3的圆周上的一定点,若在该圆周上随机取一点B,则劣弧AB的长度小于1的概率为( )
 如图,点A为周长为3的圆周上的一定点,若在该圆周上随机取一点B,则劣弧AB的长度小于1的概率为( )
如图,点A为周长为3的圆周上的一定点,若在该圆周上随机取一点B,则劣弧AB的长度小于1的概率为( )| A. | $\frac{π}{6}$ | B. | $\frac{π}{3}$ | C. | $\frac{1}{3}$ | D. | $\frac{2}{3}$ |
6.设a=0.60.6,b=0.61.5,c=1.50.6,则a,b,c的大小关系( )
| A. | a<b<c | B. | a<c<b | C. | b<a<c | D. | b<c<a |
4.若实数a、b满足条件a>b,则下列不等式一定成立的是( )
| A. | $\frac{1}{a}$<$\frac{1}{b}$ | B. | a2>b2 | C. | ab>b2 | D. | a3>b3 |
3.有这样一个有规律的步骤:对于数25,将组成它的数字和5分别取立方再求和为133,即23+53=133;对于133也做同样操作:13+33+33=55,如此反复操作,则第2017次操作后得到的数是( )
| A. | 25 | B. | 250 | C. | 55 | D. | 133 |
2.为研究女大学生体重和身高的关系,从某大学随机选取8名女大学生,其身高和体重数据如表:
利用最小二乘法求得身高预报体重的回归方程:$\widehat{y}$=0.849x-85.712,据此可求得R2≈0.64.下列说法正确的是( )
0 240714 240722 240728 240732 240738 240740 240744 240750 240752 240758 240764 240768 240770 240774 240780 240782 240788 240792 240794 240798 240800 240804 240806 240808 240809 240810 240812 240813 240814 240816 240818 240822 240824 240828 240830 240834 240840 240842 240848 240852 240854 240858 240864 240870 240872 240878 240882 240884 240890 240894 240900 240908 266669
| 身高x/cm | 165 | 165 | 157 | 170 | 175 | 165 | 155 | 170 |
| 体重y/kg | 48 | 57 | 50 | 54 | 64 | 61 | 43 | 59 |
| A. | 两组变量的相关系数为0.64 | |
| B. | R2越趋近于1,表示两组变量的相关关系越强 | |
| C. | 女大学生的身高解释了64%的体重变化 | |
| D. | 女大学生的身高差异有64%是由体重引起的 |