题目内容

2．为研究女大学生体重和身高的关系，从某大学随机选取8名女大学生，其身高和体重数据如表：
身高x/cm165165157170175165155170
体重y/kg4857505464614359
利用最小二乘法求得身高预报体重的回归方程：$\widehat{y}$=0.849x-85.712，据此可求得R2≈0.64．下列说法正确的是（　　）
A．两组变量的相关系数为0.64
B．R2越趋近于1，表示两组变量的相关关系越强
C．女大学生的身高解释了64%的体重变化
D．女大学生的身高差异有64%是由体重引起的

分析 根据题意R2≈0.64，是身高解释了64%的体重变化，由此得出结论．

解答 解：用最小二乘法求得身高预报体重的回归方程：$\widehat{y}$=0.849x-85.712，
据此可求得R2≈0.64，即“身高解释了64%的体重变化“，而随机误差贡献了剩余的36%．
故选：C．

点评 本题考查了相关指数R2的意义与应用问题，是基础题．

练习册系列答案
相关题目
12．已知两个不同的动点A，B在椭圆$\frac{y^2}{8}+\frac{x^2}{4}=1$上，且线段AB的垂直平分线恒过点P（0，-1）．求：（Ⅰ）线段AB中点M的轨迹方程；
（Ⅱ）线段AB长度的最大值．
13．函数$y=x+\frac{1}{4x}（{x＞0}）$取得最小值时，x的值为（　　）
A．$-\frac{1}{2}$B．$\frac{1}{2}$C．1D．2
10．若x，y且x+y＞2，则$\frac{1+y}{x}$和$\frac{1+x}{y}$的值满足（　　）
A．$\frac{1+y}{x}$和$\frac{1+x}{y}$都大于2B．$\frac{1+y}{x}$和$\frac{1+x}{y}$都小于2
C．$\frac{1+y}{x}$和$\frac{1+x}{y}$中至少有一个小于2D．以上说法都不对
17．函数y=ax-1（a＞0，a≠1）的图象经过点（　　）
A．（$\frac{1}{4}$，1）B．（0，1）C．（1，1）D．（$\frac{1}{2}$，1）
7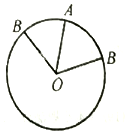．如图，点A为周长为3的圆周上的一定点，若在该圆周上随机取一点B，则劣弧AB的长度小于1的概率为（　　）
A．$\frac{π}{6}$B．$\frac{π}{3}$C．$\frac{1}{3}$D．$\frac{2}{3}$
14．在[-5，5]上随机的取一个数a，则事件“不等式x2+ax+a≥0对任意实数x恒成立”发生的概率为$\frac{2}{5}$．
11．等差数列{an}的前n项和为Sn，已知a19+2a20+a21=4，则S39=（　　）
A．38B．39C．20D．19
12．说明：请从A，B两小题中任选一题作答．
A．已知数列{an}的前n项和为Sn，且$2{S_n}={3^{n+1}}-3（{n∈{N^*}}）$．
（1）求数列{an}的通项公式；
（2）若数列{bn}满足${b_n}=\frac{1}{a_n}{log_3}{a_n}$，求数列{bn}的前n项和Tn．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网