14.下列曲线中,在x=1处切线的倾斜角为$\frac{3π}{4}$的是( )
| A. | y=x2-$\frac{3}{x}$ | B. | y=xlnx | C. | y=sin(πx) | D. | y=x3-2x2 |
13.用数学归纳法证明“凸n变形对角线的条数f(n)=$\frac{n(n-3)}{2}$”时,第一步应验证( )
| A. | n=1成立 | B. | n=2成立 | C. | n=3成立 | D. | n=4成立 |
12.为了解喜好体育运动是否与性别有关,某报记者随机采访50个路人,将调查情况进行整理后制成下表:
(1)在调查的结果中,喜好体育运动的女性有10人,不喜好体育运动的男性有5人,请将下面的2×2列联表补充完整,并判断能否在犯错误的概率不超过0.005的前提下认为喜好体育运动与性别有关?说明你的理由;
(2)若从年龄在[15,25),[25,35)的被调查者中各随机选取两人进行追踪调查,记选中的4人中不喜好体育运动的人数为X,求随机变量X的分布列和数学期望.
下面的临界值表供参考:
(参考公式:K2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$,其中n=a+b+c+d)
| 年龄(岁) | [15,25) | [25,35) | [35,45) 15 | [45,55) | [55,65) | [65,75) |
| 频数 | 5 | 10 | 8 | 10 | 5 | 5 |
| 喜好人数 | 4 | 6 | 6 | 3 | 3 |
| 喜好体育运动 | 不喜好体育运动 | 合计 | |
| 男生 | 5 | ||
| 女生 | 10 | ||
| 合计 | 50 |
下面的临界值表供参考:
| P(K2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
10.已知函数f(x)=-$\frac{2+a{x}^{2}}{{e}^{x}}$(a>0)在区间[0,1]上有极值,且函数f(x)在区间[0,1]上的最小值不小于-$\frac{7}{e}$,则a的取值范围是( )
| A. | (2,5] | B. | (2,+∞) | C. | (1,4} | D. | [5,+∞) |
9.已知函数f(x)是定义在R上的偶函数,且在区间[0,+∞)上单调递减,若f(log2a)+f(3${log}_{\frac{1}{8}}$a)≥2f(-1),则实数a的取值范围是( )
| A. | [2,4] | B. | [$\frac{1}{4}$,2] | C. | [$\frac{\sqrt{2}}{2}$,4] | D. | [$\frac{1}{2}$,2] |
7.函数y=7sin(5x-$\frac{π}{3}$)的图象可由函数y=7sin(5x-$\frac{π}{6}$)的图象( )
| A. | 向左平移$\frac{π}{6}$个单位得到 | B. | 向右平移$\frac{π}{6}$个单位得到 | ||
| C. | 向左平移$\frac{π}{30}$个单位得到 | D. | 向右平移$\frac{π}{30}$个单位得到 |
6.若将函数y=sinx+$\sqrt{3}$cosx的图象向右平移φ(φ>0)个单位长度得到函数y=sinx-$\sqrt{3}$cosx的图象,则φ的最小值为( )
| A. | $\frac{π}{6}$ | B. | $\frac{π}{2}$ | C. | $\frac{π}{3}$ | D. | $\frac{2π}{3}$ |
5. 函数y=Asin(2x+φ)(A>0,|φ|<π)在一个周期内的图象如图所示,则此函数的解析式为( )
函数y=Asin(2x+φ)(A>0,|φ|<π)在一个周期内的图象如图所示,则此函数的解析式为( )
0 240638 240646 240652 240656 240662 240664 240668 240674 240676 240682 240688 240692 240694 240698 240704 240706 240712 240716 240718 240722 240724 240728 240730 240732 240733 240734 240736 240737 240738 240740 240742 240746 240748 240752 240754 240758 240764 240766 240772 240776 240778 240782 240788 240794 240796 240802 240806 240808 240814 240818 240824 240832 266669
 函数y=Asin(2x+φ)(A>0,|φ|<π)在一个周期内的图象如图所示,则此函数的解析式为( )
函数y=Asin(2x+φ)(A>0,|φ|<π)在一个周期内的图象如图所示,则此函数的解析式为( )| A. | y=2sin(2x+$\frac{π}{3}$) | B. | y=2sin(2x-$\frac{2π}{3}$) | C. | y=2sin(2x-$\frac{π}{3}$) | D. | y=2sin(2x+$\frac{2π}{3}$) |
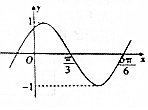 已知函数y=sin(ωx+φ)(ω>0,0<φ≤$\frac{π}{2}$)的部分图象如图所示,则cos(5ωφ)=-$\frac{1}{2}$.
已知函数y=sin(ωx+φ)(ω>0,0<φ≤$\frac{π}{2}$)的部分图象如图所示,则cos(5ωφ)=-$\frac{1}{2}$.