15.过双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1({a>0,b>0})$的左焦点F(-c,0)(c>0),作圆x2+y2=$\frac{a^2}{4}$的切线,切点为E,延长FE交双曲线右支于点P,若$\overrightarrow{OP}=2\overrightarrow{OE}-\overrightarrow{OF}$,则双曲线的离心率为( )
| A. | $\sqrt{10}$ | B. | $\frac{{\sqrt{10}}}{2}$ | C. | $\frac{{\sqrt{10}}}{5}$ | D. | $\sqrt{2}$ |
14.函数y=x3(x>0)的图象在点$({{a_k},{a_k}^3})$处的切线与x轴的交点的横坐标为ak+1,其中k∈N*,若a1=27,则a2+a4的值为( )
0 240418 240426 240432 240436 240442 240444 240448 240454 240456 240462 240468 240472 240474 240478 240484 240486 240492 240496 240498 240502 240504 240508 240510 240512 240513 240514 240516 240517 240518 240520 240522 240526 240528 240532 240534 240538 240544 240546 240552 240556 240558 240562 240568 240574 240576 240582 240586 240588 240594 240598 240604 240612 266669
| A. | 24 | B. | 16 | C. | 26 | D. | 27 |
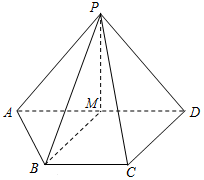 如图,在四棱锥P-ABCD中,M为AD的中点.
如图,在四棱锥P-ABCD中,M为AD的中点. 如图所示,在四棱锥P-ABCD中,平面PAD⊥平面ABCD,AB∥DC,△PAD是等边三角形,已知BD=8,AD=4,AB=2DC=4$\sqrt{5}$.
如图所示,在四棱锥P-ABCD中,平面PAD⊥平面ABCD,AB∥DC,△PAD是等边三角形,已知BD=8,AD=4,AB=2DC=4$\sqrt{5}$. 如图,半圆O的半径为1,A为直径延长线上一点,OA=2,B为半圆上任意一点,以AB为一边做等边三角形ABC,设∠AOB=θ.
如图,半圆O的半径为1,A为直径延长线上一点,OA=2,B为半圆上任意一点,以AB为一边做等边三角形ABC,设∠AOB=θ.