题目内容
13. 如图,半圆O的半径为1,A为直径延长线上一点,OA=2,B为半圆上任意一点,以AB为一边做等边三角形ABC,设∠AOB=θ.
如图,半圆O的半径为1,A为直径延长线上一点,OA=2,B为半圆上任意一点,以AB为一边做等边三角形ABC,设∠AOB=θ.(1)当$θ=\frac{π}{3}$时,求四边形OACB的面积;
(2)求线段OC长度的最大值,并指出此时θ的值.
分析 (1)利用余弦定理计算AB,分布求出△OAB和△ABC的面积即可;
(2)根据余弦定理、正弦定理用θ表示出AB,sin∠OAB,计算cos∠OAC,利用余弦定理得出OC关于θ的函数,根据三角恒等变换求出最值.
解答 解:(1)在△OAB中,由余弦定理得AB2=1+4-2×1×2×cos$\frac{π}{3}$=3,
∴AB=$\sqrt{3}$,
∴S△ABC=$\frac{1}{2}×\sqrt{3}×\sqrt{3}×\frac{\sqrt{3}}{2}$=$\frac{3\sqrt{3}}{4}$,S△AOB=$\frac{1}{2}×1×2×\frac{\sqrt{3}}{2}$=$\frac{\sqrt{3}}{2}$,
∴四边形OACB的面积为$\frac{3\sqrt{3}}{4}$+$\frac{\sqrt{3}}{2}$=$\frac{5\sqrt{3}}{4}$.
(2)由余弦定理得AB2=1+4-2×1×2×cosθ=5-4cosθ,
∴AB=$\sqrt{5-4cosθ}$,∴AC=$\sqrt{5-4cosθ}$,
由正弦定理得$\frac{AB}{sinθ}=\frac{OB}{sin∠OAB}$,即sin∠OAB=$\frac{OBsinθ}{AB}$=$\frac{sinθ}{\sqrt{5-4cosθ}}$,
∴cos∠OAB=$\frac{2-cosθ}{\sqrt{5-4cosθ}}$,
∴cos∠OAC=cos(∠OAB+$\frac{π}{3}$)=$\frac{2-cosθ}{2\sqrt{5-4cosθ}}$-$\frac{\sqrt{3}sinθ}{2\sqrt{5-4cosθ}}$,
由余弦定理得:OC2=4+5-4cosθ-2×2×$\sqrt{5-4cosθ}$×($\frac{2-cosθ}{2\sqrt{5-4cosθ}}$-$\frac{\sqrt{3}sinθ}{2\sqrt{5-4cosθ}}$)=5+2$\sqrt{3}$sinθ-2cosθ=5+4sin(θ-$\frac{π}{6}$).
∵θ∈(0,π),
∴当θ=$\frac{2π}{3}$时,OC最大,OC的最大值为3.
点评 本题考查了正弦定理和余弦定理,解三角形的应用,三角恒等变换,属于中档题.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案| A. | 0.1 | B. | 0.2 | C. | 0.6 | D. | 0.8 |
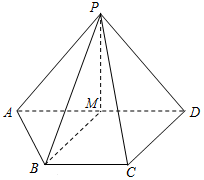 如图,在四棱锥P-ABCD中,M为AD的中点.
如图,在四棱锥P-ABCD中,M为AD的中点. 已知:三棱锥A-BCD中,平面ABD⊥平面BCD,AB⊥AD,E,F分别为BD,AD的中点.
已知:三棱锥A-BCD中,平面ABD⊥平面BCD,AB⊥AD,E,F分别为BD,AD的中点.