题目内容
15.过双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1({a>0,b>0})$的左焦点F(-c,0)(c>0),作圆x2+y2=$\frac{a^2}{4}$的切线,切点为E,延长FE交双曲线右支于点P,若$\overrightarrow{OP}=2\overrightarrow{OE}-\overrightarrow{OF}$,则双曲线的离心率为( )| A. | $\sqrt{10}$ | B. | $\frac{{\sqrt{10}}}{2}$ | C. | $\frac{{\sqrt{10}}}{5}$ | D. | $\sqrt{2}$ |
分析 通过双曲线的特点知原点O为两焦点的中点,利用中位线的性质,求出PF′的长度及判断出PF′垂直于PF,通过勾股定理得到a,c的关系,进而求出双曲线的离心率.
解答 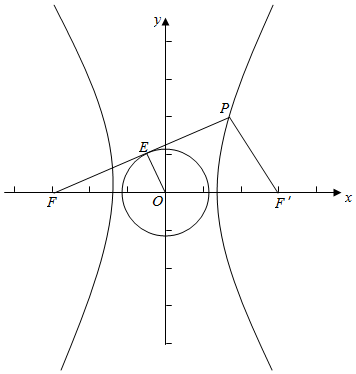 解:如图,记右焦点为F′,
解:如图,记右焦点为F′,
则O为FF′的中点,
∵$\overrightarrow{OP}=2\overrightarrow{OE}-\overrightarrow{OF}$,
即为$\overrightarrow{OP}$+$\overrightarrow{OF}$=2$\overrightarrow{OE}$,
可得E为PF的中点,
∴OE为△FF′P的中位线,
∴PF′=2OE=a,
∵E为切点,
∴OE⊥PF,
∴PF′⊥PF,
∵点P在双曲线上,
∴PF-PF′=2a,
∴PF=PF′+2a=3a,
在Rt△PFF′中,有:PF2+PF′2=FF′2,
∴9a2+a2=4c2,即10a2=4c2,
∴离心率e=$\frac{c}{a}$=$\sqrt{\frac{{c}^{2}}{{a}^{2}}}$=$\sqrt{\frac{10}{4}}$=$\frac{\sqrt{10}}{2}$,
故选:B.
点评 本题主要考查双曲线的简单性质、圆的方程等基础知识,考查运算求解能力,考查数形结合思想、化归与转化思想,在圆锥曲线中,求离心率关键就是求三参数a,b,c的关系,注意解题方法的积累,属于中档题.

练习册系列答案
相关题目
6.设集合A={x|-1<x<3},B={x|x2+x-2>0},则A∩B=( )
| A. | (2,3) | B. | (1,3) | C. | (-∞,-2)∪(1,3) | D. | (-∞,-2)∪(1,+∞) |
7.若直线(a+1)x-y+1-2a=0与(a2-1)x+(a-1)y-15=0平行,则实数a的值等于( )
| A. | 1或-1 | B. | 1 | C. | -1 | D. | 不存在 |
15.数列1,37,314,321,…中,398是这个数列的( )
| A. | 第15项 | B. | 第14项 | C. | 第13项 | D. | 不在此数列中 |
 如图,在四棱锥P-ABCD中,在底面ABCD中,AD∥BC,AD⊥CD,Q是AD的中点,M是棱PC的中点,PA=PD=2,BC=$\frac{1}{2}$AD=1,CD=$\sqrt{3}$,PB=$\sqrt{6}$.
如图,在四棱锥P-ABCD中,在底面ABCD中,AD∥BC,AD⊥CD,Q是AD的中点,M是棱PC的中点,PA=PD=2,BC=$\frac{1}{2}$AD=1,CD=$\sqrt{3}$,PB=$\sqrt{6}$.