题目内容

18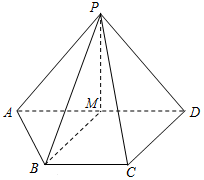．如图，在四棱锥P-ABCD中，M为AD的中点．
（1）若AD∥BC，AD=2BC，求证：BM∥平面PCD；
（2）若PA=PD，平面PAD⊥平面PBM，求证：AD⊥PB．

分析 1）只需证明四边形BCDM为平行四边形，即可得CD∥BM，BM∥平面PCD．  
（2）只需证明PM⊥AD，AD⊥平面PBM，即可得AD⊥PB．

解答 证明：（1）因为AD∥BC，AD=2BC，M为AD中点，
所以BC∥MD，且BC=MD，
所以四边形BCDM为平行四边形，
故CD∥BM，
又BM?平面PCD，CD?平面PCD，
所以BM∥平面PCD．  
（2）因为PA=PD，M为AD中点，
所以PM⊥AD，
又平面PAD⊥平面PBM，平面PAD∩平面PBM=PM，AD?平面PAD，
所以AD⊥平面PBM．
又PB?平面PBM，
所以AD⊥PB．                             

点评 本题考查了空间线面平行、线线垂直的判定，属于中档题．

练习册系列答案
相关题目
8．函数y=$\frac{lg|x|}{x}$的图象大致是（　　）
A．B．C．D．
9．设集合A={x|-1＜x＜3}，B={x|x≥1}，则A∩B=（　　）
A．（-1，1]B．[1，3）C．[-1，3]D．（-1，+∞）
6．设函数f（x）=g（x）+x2，曲线y=g（x）在点（1，g（1））处的切线方程为9x+y-1=0，则曲线y=f（x）在点（1，f（1））处的切线方程为7x+y=0．
13．如图，半圆O的半径为1，A为直径延长线上一点，OA=2，B为半圆上任意一点，以AB为一边做等边三角形ABC，设∠AOB=θ．
（1）当$θ=\frac{π}{3}$时，求四边形OACB的面积；
（2）求线段OC长度的最大值，并指出此时θ的值．
3．已知正项数列{an}的前n项和为Sn，点（an，Sn）（n∈N*）都在函数f（x）=$\frac{1}{4}{x^2}+\frac{1}{2}x-\frac{15}{4}$的图象上．
（1）求数列{an}的通项公式；
（2）若bn=an•3n，求数列{bn}的前n项和Tn．
10．已知向量$\overrightarrow{a}$=（3，4），$\overrightarrow{b}$=（-1，2）．
（1）求向量$\overrightarrow{a}$与$\overrightarrow{b}$夹角的余弦值；
（2）若向量$\overrightarrow{a}$-λ$\overrightarrow{b}$与$\overrightarrow{a}$+2$\overrightarrow{b}$平行，求λ的值．
7．已知双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{2}$=1（a＞0）和抛物线y2=8x有相同的焦点，则双曲线的离心率为$\sqrt{2}$．
18．若复数Z的共轭复数为$\overline Z$，且满足：$\frac{\overline Z}{1+i}$=1+i，其中i为虚数单位，则|Z|=（　　）
A．1B．2C．$\sqrt{2}$D．4

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网