1.用反证法证明:若整系数一元二次方程ax2+bx+c=0(a≠0)有有理数根,那么a,b,c中至少有一个是偶数.用反证法证明时,下列假设正确的是( )
| A. | 假设a,b,c都是偶数 | B. | 假设a,b,c都不是偶数 | ||
| C. | 假设a,b,c至多有一个偶数 | D. | 假设a,b,c至多有两个偶数 |
16.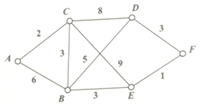 某市A,B,C,D,E,F六个城区欲架设光缆,如图所示,两点之间的线段及线段上的相应数字分别对应城区可以架设光缆及所需光缆的长度,如果任意两个城市之间均匀光缆相通,则所需光缆的总长度的最小值是( )
某市A,B,C,D,E,F六个城区欲架设光缆,如图所示,两点之间的线段及线段上的相应数字分别对应城区可以架设光缆及所需光缆的长度,如果任意两个城市之间均匀光缆相通,则所需光缆的总长度的最小值是( )
 某市A,B,C,D,E,F六个城区欲架设光缆,如图所示,两点之间的线段及线段上的相应数字分别对应城区可以架设光缆及所需光缆的长度,如果任意两个城市之间均匀光缆相通,则所需光缆的总长度的最小值是( )
某市A,B,C,D,E,F六个城区欲架设光缆,如图所示,两点之间的线段及线段上的相应数字分别对应城区可以架设光缆及所需光缆的长度,如果任意两个城市之间均匀光缆相通,则所需光缆的总长度的最小值是( )| A. | 10 | B. | 12 | C. | 14 | D. | 15 |
15. 某市A,B,C,D,E,F六个城区欲架设光缆,如图所示,两点之间的线段及线段上的相应数字分别表示对应城区可以架设光缆及所需光缆的长度,如果任意两个城市之间均有光缆相通,则所需光缆的总长度的最小值是( )
某市A,B,C,D,E,F六个城区欲架设光缆,如图所示,两点之间的线段及线段上的相应数字分别表示对应城区可以架设光缆及所需光缆的长度,如果任意两个城市之间均有光缆相通,则所需光缆的总长度的最小值是( )
 某市A,B,C,D,E,F六个城区欲架设光缆,如图所示,两点之间的线段及线段上的相应数字分别表示对应城区可以架设光缆及所需光缆的长度,如果任意两个城市之间均有光缆相通,则所需光缆的总长度的最小值是( )
某市A,B,C,D,E,F六个城区欲架设光缆,如图所示,两点之间的线段及线段上的相应数字分别表示对应城区可以架设光缆及所需光缆的长度,如果任意两个城市之间均有光缆相通,则所需光缆的总长度的最小值是( )| A. | 12 | B. | 13 | C. | 14 | D. | 15 |
14.计算定积分${∫}_{1}^{3}$(2x-$\frac{1}{x^2}$)dx的值是( )
| A. | 0 | B. | $\frac{22}{3}$ | C. | $\frac{11}{3}$ | D. | $\frac{3}{11}$ |
13.给出以下结论:
(1)直线a∥平面α,直线b?α,则a∥b.
(2)若a?α,b?α,则a、b无公点.
(3)若a?α,则a∥α或a与α相交
(4)若a∩α=A,则a?α.
正确的个数为( )
(1)直线a∥平面α,直线b?α,则a∥b.
(2)若a?α,b?α,则a、b无公点.
(3)若a?α,则a∥α或a与α相交
(4)若a∩α=A,则a?α.
正确的个数为( )
| A. | 1个 | B. | 4个 | C. | 3个 | D. | 2个 |
12.定义区间(a,b)、[a,b)、(a,b]、[a,b]的长度均为d=b-a,多个区间并集的长度为各区间长度之和,例如,(1,2)∪[3,5)的长度为d=(2-1)+(5-3)=3,用[x]表示不超过的x最大整数,记{x}=x-[x],其中x∈R.设f(x)=[x]•{x},g(x)=2x-[x]-2,若用d1,d2,d3分别表示不等式f(x)>g(x)、方程f(x)=g(x)、不等式f(x)<g(x)解集的长度,则当0≤x≤2016时,有( )
0 240157 240165 240171 240175 240181 240183 240187 240193 240195 240201 240207 240211 240213 240217 240223 240225 240231 240235 240237 240241 240243 240247 240249 240251 240252 240253 240255 240256 240257 240259 240261 240265 240267 240271 240273 240277 240283 240285 240291 240295 240297 240301 240307 240313 240315 240321 240325 240327 240333 240337 240343 240351 266669
| A. | d1=2,d2=0,d3=2014 | B. | d1=2,d2=2,d3=2014 | ||
| C. | d1=2,d2=1,d3=2013 | D. | d1=2,d2=2,d3=2012 |