题目内容
1．用反证法证明：若整系数一元二次方程ax2+bx+c=0（a≠0）有有理数根，那么a，b，c中至少有一个是偶数．用反证法证明时，下列假设正确的是（ ）| A． | 假设a，b，c都是偶数 | B． | 假设a，b，c都不是偶数 | ||
| C． | 假设a，b，c至多有一个偶数 | D． | 假设a，b，c至多有两个偶数 |
分析 本题考查反证法的概念，逻辑用语，否命题与命题的否定的概念，逻辑词语的否定．根据反证法的步骤，假设是对原命题结论的否定，故只须对“b、c中至少有一个偶数”写出否定即可．
解答 解：根据反证法的步骤，假设是对原命题结论的否定
“至少有一个”的否定“都不是”．
即假设正确的是：假设a、b、c都不是偶数
故选：B．
点评 一些正面词语的否定：“是”的否定：“不是”；“能”的否定：“不能”；“都是”的否定：“不都是”；“至多有一个”的否定：“至少有两个”；“至少有一个”的否定：“一个也没有”；“是至多有n个”的否定：“至少有n+1个”；“任意的”的否定：“某个”；“任意两个”的否定：“某两个”；“所有的”的否定：“某些”．
练习册系列答案
相关题目
2．i是虚数单位，则复数$\frac{i}{1+i}$的虚部是（ ）
| A． | $\frac{1}{2}$ | B． | $\frac{1}{2}i$ | C． | $-\frac{1}{2}$ | D． | $-\frac{1}{2}i$ |
16．
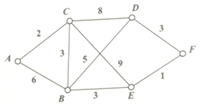某市A，B，C，D，E，F六个城区欲架设光缆，如图所示，两点之间的线段及线段上的相应数字分别对应城区可以架设光缆及所需光缆的长度，如果任意两个城市之间均匀光缆相通，则所需光缆的总长度的最小值是（ ）
某市A，B，C，D，E，F六个城区欲架设光缆，如图所示，两点之间的线段及线段上的相应数字分别对应城区可以架设光缆及所需光缆的长度，如果任意两个城市之间均匀光缆相通，则所需光缆的总长度的最小值是（ ）| A． | 10 | B． | 12 | C． | 14 | D． | 15 |
13．若函数f（x）=$\frac{1}{2}{x^2}$+lnx-ax+1在区间（$\frac{1}{2}$，3）上单调递减，则实数a的取值范围为（ ）
| A． | （-∞，2] | B． | （-∞，2） | C． | [3，+∞） | D． | $（-∞，\frac{5}{2}）$ |