1.已知球O是正三棱锥(底面为正三角形,顶点在底面的射影为底面中心)A-BCD的外接球,BC=3,$AB=2\sqrt{3}$,点E在线段BD上,且BD=3BE,过点E作圆O的截面,则所得截面圆面积的取值范围是( )
| A. | [π,4π] | B. | [2π,4π] | C. | [3π,4π] | D. | (0,4π] |
20.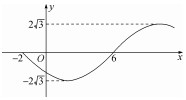 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<π)的部分图象如图所示,则函数g(x)=Acos(φx+ω)图象的一个对称中心可能为( )
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<π)的部分图象如图所示,则函数g(x)=Acos(φx+ω)图象的一个对称中心可能为( )
 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<π)的部分图象如图所示,则函数g(x)=Acos(φx+ω)图象的一个对称中心可能为( )
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<π)的部分图象如图所示,则函数g(x)=Acos(φx+ω)图象的一个对称中心可能为( )| A. | $(-\frac{5}{2},0)$ | B. | $(\frac{1}{6},0)$ | C. | $(-\frac{1}{2},0)$ | D. | $(-\frac{11}{6},0)$ |
19.若倾斜角为α的直线l与曲线y=x4相切于点(1,1),则cos2α-sin2α的值为( )
| A. | $-\frac{1}{2}$ | B. | 1 | C. | $-\frac{3}{5}$ | D. | $-\frac{7}{17}$ |
18.某学校上午安排上四节课,每节课时间为40分钟,第一节课上课时间为8:00~8:40,课间休息10分钟.某学生因故迟到,若他在9:10~10:00之间到达教室,则他听第二节课的时间不少于10分钟的概率为( )
| A. | $\frac{1}{5}$ | B. | $\frac{3}{10}$ | C. | $\frac{2}{5}$ | D. | $\frac{4}{5}$ |
17.已知双曲线C1:$\frac{x^2}{4}-\frac{y^2}{3}=1$与双曲线C2:$\frac{x^2}{4}-\frac{y^2}{3}=-1$,给出下列说法,其中错误的是( )
| A. | 它们的焦距相等 | B. | 它们的焦点在同一个圆上 | ||
| C. | 它们的渐近线方程相同 | D. | 它们的离心率相等 |
16.下列函数中,与函数y=x3的单调性和奇偶性一致的函数是( )
0 239906 239914 239920 239924 239930 239932 239936 239942 239944 239950 239956 239960 239962 239966 239972 239974 239980 239984 239986 239990 239992 239996 239998 240000 240001 240002 240004 240005 240006 240008 240010 240014 240016 240020 240022 240026 240032 240034 240040 240044 240046 240050 240056 240062 240064 240070 240074 240076 240082 240086 240092 240100 266669
| A. | $y=\sqrt{x}$ | B. | y=tanx | C. | $y=x+\frac{1}{x}$ | D. | y=ex-e-x |