题目内容
20.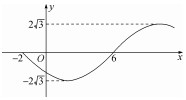 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<π)的部分图象如图所示,则函数g(x)=Acos(φx+ω)图象的一个对称中心可能为( )
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<π)的部分图象如图所示,则函数g(x)=Acos(φx+ω)图象的一个对称中心可能为( )| A. | $(-\frac{5}{2},0)$ | B. | $(\frac{1}{6},0)$ | C. | $(-\frac{1}{2},0)$ | D. | $(-\frac{11}{6},0)$ |
分析 由函数的图象的顶点坐标求出A,由周期求出ω,由五点法作图求出φ的值,可得g(x)的解析式,再利用正弦函数的图象的对称性,求得函数g(x)=Acos(φx+ω)图象的一个对称中心.
解答 解:根据函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<π)的部分图象,
可得A=2$\sqrt{3}$,$\frac{2π}{ω}$=2(6+2),∴ω=$\frac{π}{8}$.
再根据五点法作图可得$\frac{π}{8}$•6+φ=π,∴φ=$\frac{π}{4}$,∴f(x)=2$\sqrt{3}$sin($\frac{π}{8}$x+$\frac{π}{4}$).
则函数g(x)=Acos(φx+ω)=2$\sqrt{3}$cos($\frac{π}{4}$x+$\frac{π}{8}$)图象的一个对称中心可能(-$\frac{1}{2}$,0),
故选:C.
点评 本题主要考查由函数y=Asin(ωx+φ)的部分图象求解析式,由函数的图象的顶点坐标求出A,由周期求出ω,由五点法作图求出φ的值,正弦函数的图象的对称性,属于基础题.

练习册系列答案
相关题目
10.在底面ABCD为平行四边形的四棱柱ABCD-A1B1C1D1中,M是AC与BD的交点,若$\overrightarrow{AB}$=$\overrightarrow a$,$\overrightarrow{{A_1}{D_1}}$=$\overrightarrow b$,$\overrightarrow{{A_1}A}$=$\overrightarrow c$,则下列向量中与$\overrightarrow{{B_1}M}$相等的向量是( )
| A. | $-\frac{1}{2}\overrightarrow a+\frac{1}{2}\overrightarrow b+\overrightarrow c$ | B. | $\frac{1}{2}\overrightarrow a+\frac{1}{2}\overrightarrow b+\overrightarrow c$ | C. | $\frac{1}{2}\overrightarrow a-\frac{1}{2}\overrightarrow b+\overrightarrow c$ | D. | $-\frac{1}{2}\overrightarrow a-\frac{1}{2}\overrightarrow b+\overrightarrow c$ |
11.将函数$f(x)=2sin(\frac{x}{3}-\frac{π}{6})$的图象向左平移$\frac{π}{4}$个单位,再向上平移2个单位,得到函数g(x)的图象,则g(x)的解析式为( )
| A. | $g(x)=2sin(\frac{x}{3}-\frac{π}{4})-2$ | B. | $g(x)=2sin(\frac{x}{3}+\frac{π}{4})+2$ | C. | $g(x)=2sin(\frac{x}{3}-\frac{π}{12})+2$ | D. | $g(x)=2sin(\frac{x}{3}-\frac{π}{12})-2$ |
15.已知集合A={x∈N|-2<x<4},$B=\{x|\frac{1}{2}≤{2^x}≤4\}$,则A∩B=( )
| A. | {x|-1≤x≤2} | B. | {-1,0,1,2} | C. | {1,2} | D. | {0,1,2} |
12.我国古代名著《九章算术》中有这样一段话:“今有金锤,长五尺,斩本一尺,重四斤.斩末一尺,重二斤.”意思是:“现有一根金锤,头部的1尺,重4斤;尾部的1尺,重2斤;且从头到尾,每一尺的重量构成等差数列.”则下列说法错误的是( )
| A. | 该金锤中间一尺重3斤 | |
| B. | 中间三尺的重量和是头尾两尺重量和的3倍 | |
| C. | 该金锤的重量为15斤 | |
| D. | 该金锤相邻两尺的重量之差的绝对值为0.5斤 |
10.曲线y=lgx在x=1处的切线斜率是( )
| A. | $\frac{1}{ln10}$ | B. | ln10 | C. | lne | D. | $\frac{1}{lne}$ |