若倾斜角为α的直线l与曲线y=x4相切于点(1.1).则cos2α-sin2α的值为( )A．$-\frac{1}{2}$B．1C．$-\frac{3}{5}$D．$-\frac{7}{17}$ 题目和参考答案——青夏教育精英家教网—

题目内容

19．若倾斜角为α的直线l与曲线y=x⁴相切于点（1，1），则cos²α-sin2α的值为（　　）

A．

$-\frac{1}{2}$

B．

C．

$-\frac{3}{5}$

D．

$-\frac{7}{17}$

分析由条件利用同角三角函数的基本关系，求得cos²α-sin2α的值．

解答解：y′=4x³，
故y′|_x=1=4，
即tanα=4，
则cos²α-sin2α
=$\frac{{cos}^{2}α-2sinαcosα}{{sin}^{2}α{+cos}^{2}α}$
=$\frac{1-2tanα}{{tan}^{2}α+1}$
=$\frac{1-2×4}{16+1}$
=-$\frac{7}{17}$，
故选：D．

点评本题主要考查同角三角函数的基本关系，属于基础题．

练习册系列答案

68所名校图书小升初高分夺冠真卷系列答案

10．若不等式a＞|x-5|-|x+1|对x∈R恒成立，则实数a的取值范围是（6，+∞）．

7．已知$\overrightarrow a=（{1，λ}），\overrightarrow b=（{2，1}）$，若向量$2\overrightarrow a+\overrightarrow b$与$\overrightarrow c=（{8，6}）$共线，则$\overrightarrow a$在$\overrightarrow b$方向上的投影为$\frac{3\sqrt{5}}{5}$．

14．已知直线l的参数方程为$\left\{\begin{array}{l}x=4+\frac{{\sqrt{2}}}{2}t\\ y=\frac{{\sqrt{2}}}{2}t\end{array}\right.$（t为参数），以坐标原点为极点，x轴的非负半轴为极轴，建立极坐标系，圆C的极坐标方程为ρ=4cosθ，直线l与圆C交于A，B两点．
（1）求圆C的直角坐标方程及弦AB的长；
（2）动点P在圆C上（不与A，B重合），试求△ABP的面积的最大值．

4．在△ABC中，角A，B，C的对边分别为a，b，c，$-\frac{c}{cosB}$是$\frac{b}{cosB}$与$\frac{a}{cosA}$的等差中项且a=8，△ABC的面积为$4\sqrt{3}$，则b+c的值为$4\sqrt{5}$．

11．已知函数f（x）=|2x-1|+|x+1|．
（1）求函数f（x）的值域M；
（2）若a∈M，试比较|a-1|+|a+1|，$\frac{3}{2a}$，$\frac{7}{2}-2a$的大小．

8．已知椭圆E：$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1（a＞b＞0）的左、右焦点分别为F₁、F₂，A为椭圆E的右顶点，B，C分别为椭圆E的上、下顶点．线段CF₂的延长线与线段AB交于点M，与椭圆E交于点P．
（1）若椭圆的离心率为$\frac{{\sqrt{2}}}{2}$，△PF₁C的面积为12，求椭圆E的方程；
（2）设S${\;}_{△CM{F}_{2}}$=λ•S${\;}_{△CP{F}_{1}}$，求实数λ的最小值．

9．

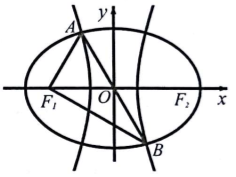如图，F₁、F₂是椭圆C₁与双曲线C₂的公共焦点，A、B分别是C₁、C₂在第二、四象限的公共点，若AF₁⊥BF₁，且∠AF₁O=$\frac{π}{3}$，则C₁与C₂的离心率之和为（　　）

试题分类