7.设i为虚数单位,则复数(-2i-1)•i的共轭复数为( )
| A. | -2-i | B. | 2-i | C. | -2+i | D. | 2+i |
6.设集合A={-2,-1,1,2},B={-3,-1,0,2},则A∩B的元素的个数为( )
| A. | 2 | B. | 3 | C. | 4 | D. | 1 |
3.某工厂为了解用电量y与气温x℃之间的关系,随机统计了5天的用电量与当天平均气温,得到如下统计表:
$\sum_{i=1}^{5}$xiyi=5446,$\sum_{i=1}^{5}$xi2=4538,$\widehat{b}$=$\frac{\sum_{i=1}^{5}{x}_{i}{y}_{i}-5\overline{x}\overline{y}}{\sum_{i=1}^{5}{{x}_{i}}^{2}-5{\overline{x}}^{2}}$,$\widehat{a}$=$\overline{y}$-$\widehat{b}$$\overline{x}$
(1)请根据表中的数据,求出y关于x的线性回归方程,据气象预报9月3日的平均气温是23℃,请预测9月3日的用电量;(结果保留整数)
(2)从表中任选两天,求用电量(万度)都超过35的概率.
| 日期 | 8月1日 | 8月7日 | 8月14日 | 8月18日 | 8月25日 |
| 平均气温(℃) | 33 | 30 | 32 | 30 | 25 |
| 用电量(万度) | 38 | 35 | 41 | 36 | 30 |
(1)请根据表中的数据,求出y关于x的线性回归方程,据气象预报9月3日的平均气温是23℃,请预测9月3日的用电量;(结果保留整数)
(2)从表中任选两天,求用电量(万度)都超过35的概率.
1.已知f(x)是定义在R上的奇函数,当x>0时,f(x)=2x-6,则f(f(2))=( )
| A. | -$\frac{23}{4}$ | B. | $\frac{23}{4}$ | C. | -2 | D. | 2 |
18.在2016年高考结束后,针对高考成绩是否达到了考生自己预期水平的情况,某校在高三部分毕业生内部进行了抽样调查,现从高三年级A、B、C、D、E、F六个班随机抽取了50人,将统计结果制成了如下的表格:
(Ⅰ)根据上述的表格,估计该校高三学生2016年的高考成绩达到自己的预期水平的概率;
(Ⅱ)若从E班、F班的抽取对象中,进一步各班随机选取2名同学进行详细调查,记选取的4人中,高考成绩没有达到预期水平的人数为ξ,求随机变量ξ的分布列和数学期望.
0 239880 239888 239894 239898 239904 239906 239910 239916 239918 239924 239930 239934 239936 239940 239946 239948 239954 239958 239960 239964 239966 239970 239972 239974 239975 239976 239978 239979 239980 239982 239984 239988 239990 239994 239996 240000 240006 240008 240014 240018 240020 240024 240030 240036 240038 240044 240048 240050 240056 240060 240066 240074 266669
| 班级 | A | B | C | D | E | F |
| 抽取人数 | 6 | 10 | 12 | 12 | 6 | 4 |
| 其中达到预期水平的人数 | 3 | 6 | 6 | 6 | 4 | 3 |
(Ⅱ)若从E班、F班的抽取对象中,进一步各班随机选取2名同学进行详细调查,记选取的4人中,高考成绩没有达到预期水平的人数为ξ,求随机变量ξ的分布列和数学期望.
 已知函数f(x)=sin(ωx+φ)(ω>0)的图象如图所示,则f(4)=$\frac{\sqrt{2}}{2}$.
已知函数f(x)=sin(ωx+φ)(ω>0)的图象如图所示,则f(4)=$\frac{\sqrt{2}}{2}$.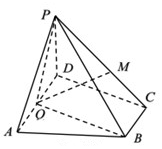 如图在四棱锥P-ABCD中,底面ABCD为直角梯形,AD∥BC,∠ADC=90°,平面PAD⊥底面ABCD,Q为AD的中点,M是棱PC上的一点,PA=PD=4=AD=2BC,CD=2.
如图在四棱锥P-ABCD中,底面ABCD为直角梯形,AD∥BC,∠ADC=90°,平面PAD⊥底面ABCD,Q为AD的中点,M是棱PC上的一点,PA=PD=4=AD=2BC,CD=2.