题目内容
19.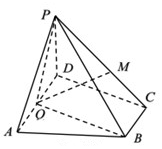 如图在四棱锥P-ABCD中,底面ABCD为直角梯形,AD∥BC,∠ADC=90°,平面PAD⊥底面ABCD,Q为AD的中点,M是棱PC上的一点,PA=PD=4=AD=2BC,CD=2.
如图在四棱锥P-ABCD中,底面ABCD为直角梯形,AD∥BC,∠ADC=90°,平面PAD⊥底面ABCD,Q为AD的中点,M是棱PC上的一点,PA=PD=4=AD=2BC,CD=2.(Ⅰ)求证:平面PQB⊥平面PAD;
(Ⅱ)若二面角M-BQ-C为30°,设|PM|=t|MC|,试确定t的值.
分析 (Ⅰ)由已知可得PQ⊥AD,再由面面垂直的性质可得PQ⊥平面ABCD,得到PQ⊥BQ,再由已知可得BQ⊥AD,结合线面垂直的判定可得BQ⊥平面PAD,从而得到平面PQB⊥平面PAD;
(Ⅱ)由(Ⅰ)可知,QB、AD、QP两两互相垂直,以Q为坐标原点,分别以QA、QB、QP为x、y、z轴距离空间直角坐标系,可得则Q(0,0,0),P(0,0,$2\sqrt{3}$),C(-2,2,0),由|PM|=t|MC|,得M($-\frac{2t}{t+1},\frac{2t}{t+1},\frac{2\sqrt{3}}{t+1}$).求出平面MQB与平面CBQ的一个法向量,由两法向量所成角的余弦值结合已知列式求得t值.
解答 (Ⅰ)证明:如图,
∵PA=PD,Q为AD的中点,
∴PQ⊥AD,又平面PAD⊥底面ABCD,且平面PAD∩底面ABCD=AD,
∴PQ⊥平面ABCD,而BQ?平面ABCD,
∴PQ⊥BQ,
又底面ABCD为直角梯形,∠ADC=90°,
∴CD⊥AD,
∵BC∥AD,BC=$\frac{1}{2}AD=2$,
∴四边形QBCD为平行四边形,则BQ∥CD,得BQ⊥AD,
又PQ∩AD=Q,∴BQ⊥平面PAD,
∵BQ?平面PBQ,则平面PQB⊥平面PAD;
(Ⅱ)由(Ⅰ)可知,QB、AD、QP两两互相垂直,
以Q为坐标原点,分别以QA、QB、QP为x、y、z轴距离空间直角坐标系,
则Q(0,0,0),P(0,0,$2\sqrt{3}$),C(-2,2,0),
∵|PM|=t|MC|,∴$\overrightarrow{PM}=t\overrightarrow{MC}$,可得M($-\frac{2t}{t+1},\frac{2t}{t+1},\frac{2\sqrt{3}}{t+1}$).
$\overrightarrow{QB}=(0,2,0)$,$\overrightarrow{QM}$=($-\frac{2t}{t+1},\frac{2t}{t+1},\frac{2\sqrt{3}}{t+1}$).
设平面MQB的一个法向量为$\overrightarrow{m}=(x,y,z)$,
由$\left\{\begin{array}{l}{\overrightarrow{m}•\overrightarrow{QB}=0}\\{\overrightarrow{m}•\overrightarrow{QM}=0}\end{array}\right.$,得$\left\{\begin{array}{l}{2y=0}\\{-\frac{2t}{t+1}x+\frac{2t}{t+1}y+\frac{2\sqrt{3}}{t+1}z=0}\end{array}\right.$,取z=1,得$\overrightarrow{m}=(\frac{\sqrt{3}}{t},0,1)$.
由图可知,平面CBQ的一个法向量$\overrightarrow{n}=(0,0,1)$.
由|cos<$\overrightarrow{m},\overrightarrow{n}$>|=|$\frac{\overrightarrow{m}•\overrightarrow{n}}{|\overrightarrow{m}||\overrightarrow{n}|}$|=|$\frac{1}{1×\sqrt{\frac{3}{{t}^{2}}+1}}$|=cos30$°=\frac{\sqrt{3}}{2}$,解得t=3.
点评 本题考查面面垂直的判定,考查了空间想象能力和思维能力,训练了利用空间向量求二面角的平面角,是中档题.

| A. | $\sqrt{e}$ | B. | 2 | C. | e | D. | 3 |
| A. | f(x)=ln(-x)+2x+1 | B. | f(x)=-ln(-x)-2x+1 | C. | f(x)=-ln(-x)-2x-1 | D. | f(x)=-ln(-x)+2x-1 |
| A. | 1 | B. | -1 | C. | e | D. | -e |