题目内容
4.已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)过点($\sqrt{2}$,1),且焦距为2$\sqrt{2}$.(1)求椭圆C的方程;
(2)若直线l:y=k(x+1)与椭圆C相交于不同的两点A、B,定点P的坐标为($\frac{1}{4}$,0),证明:$\overrightarrow{PA}$•$\overrightarrow{PB}$+$\frac{4}{2{k}^{2}+1}$是常数.
分析 (1)利用椭圆的离心率公式求得a2=b2+2,将点代入椭圆方程,即可求得a和b的值,求得椭圆方程;
(2)将直线代入椭圆方程,利用韦达定理及向量数量积的坐标运算,即可求得$\overrightarrow{PA}$•$\overrightarrow{PB}$+$\frac{4}{2{k}^{2}+1}$是常数.
解答 解:(1)由题意可知:2c=2$\sqrt{2}$,则c=$\sqrt{2}$,则a2=b2+2,
将($\sqrt{2}$,1),代入椭圆方程可得:$\frac{2}{{b}^{2}+2}+\frac{1}{{b}^{2}}=1$,解得:b2=2,则a2=4,
∴椭圆的标准方程:$\frac{{x}^{2}}{4}+\frac{{y}^{2}}{2}=1$;
(2)证明:由$\left\{\begin{array}{l}{y=k(x+1)}\\{{x}^{2}+2{y}^{2}=4}\end{array}\right.$,整理得:(2k2+1)x2+4k2x+2k2-4=0,
设A(x1,y1),B(x2,y2),则x1+x2=-$\frac{4{k}^{2}}{2{k}^{2}+1}$,x1x2=$\frac{2{k}^{2}-4}{2{k}^{2}+1}$,
由$\overrightarrow{PA}$=(x1-$\frac{1}{4}$,y1),$\overrightarrow{PB}$=(x2-$\frac{1}{4}$,y2),
$\overrightarrow{PA}$•$\overrightarrow{PB}$+$\frac{4}{2{k}^{2}+1}$=(x1-$\frac{1}{4}$)(x2-$\frac{1}{4}$)+y1y2+$\frac{4}{2{k}^{2}+1}$,
=(x1-$\frac{1}{4}$)(x2-$\frac{1}{4}$)+k2(x1+1)(x1+1)+$\frac{4}{2{k}^{2}+1}$,
=(1+k2)x1x2+(k2-$\frac{1}{4}$)(x1+x2)+$\frac{4}{2{k}^{2}+1}$+k2+$\frac{1}{16}$,
=(1+k2)×$\frac{2{k}^{2}-4}{2{k}^{2}+1}$+(k2-$\frac{1}{4}$)(-$\frac{4{k}^{2}}{2{k}^{2}+1}$)+$\frac{4}{2{k}^{2}+1}$+k2+$\frac{1}{16}$,
=$\frac{1}{16}$,
∴$\overrightarrow{PA}$•$\overrightarrow{PB}$+$\frac{4}{2{k}^{2}+1}$是常数.
点评 本题考查椭圆的标准方程,直线与椭圆的位置关系,考查韦达定理,向量数量积的坐标运算,考查计算能力,属于中档题.

 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案 已知输入的x=11,执行如图所示的程序框图,则输出的x的值为( )
已知输入的x=11,执行如图所示的程序框图,则输出的x的值为( )| A. | 12 | B. | 23 | C. | 47 | D. | 95 |
| A. | ¬p:?x∈R,log5x<0 | B. | ¬p:?x∈R,log5x≤0 | C. | ¬p:?x∈R,log5x≤0 | D. | ¬p:?x∈R,log5x<0 |
| 班级 | A | B | C | D | E | F |
| 抽取人数 | 6 | 10 | 12 | 12 | 6 | 4 |
| 其中达到预期水平的人数 | 3 | 6 | 6 | 6 | 4 | 3 |
(Ⅱ)若从A班、F班,从抽查到的达到预期水平的所有对象中,再随机选取2名同学进行详细调查,求选取的2人中含有A班同学的概率.
| A. | {-1} | B. | {0} | C. | {-1,0} | D. | {-1,0,1} |
| A. | n+(n+1)+(n+2)+…+(3n-2)=n2 | B. | n+(n+1)+(n+2)+…+(3n-2)=(2n-1)2 | ||
| C. | n+(n+1)+(n+2)+…+(3n-1)=n2 | D. | n+(n+1)+(n+2)+…+(3n-1)=(2n-1)2 |
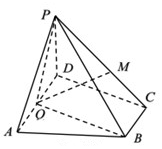 如图在四棱锥P-ABCD中,底面ABCD为直角梯形,AD∥BC,∠ADC=90°,平面PAD⊥底面ABCD,Q为AD的中点,M是棱PC上的一点,PA=PD=4=AD=2BC,CD=2.
如图在四棱锥P-ABCD中,底面ABCD为直角梯形,AD∥BC,∠ADC=90°,平面PAD⊥底面ABCD,Q为AD的中点,M是棱PC上的一点,PA=PD=4=AD=2BC,CD=2.